Circunferencia
Instrucciones:
Leer con atención cada uno de los enunciados y seleccionar la opción correcta, inmediatamente el sistema proporcionará una realimentación que hay que atender.
Circunferencia1.- El radio y las coordenads del centro de la circunferencia de ecuació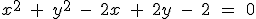n 
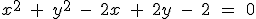, son
, son
| |
| |
| |
|
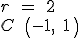
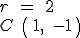
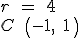
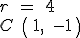
2.- La ecuación de la circunferencia con centro en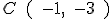 
y que contiene al punto de coordenadas 
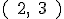, es
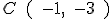y que contiene al punto de coordenada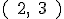s , es
| |
| |
| |
|
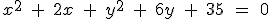
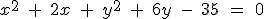
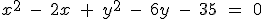
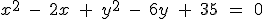
3.- La ecuación de la circunferencia que tiene centro en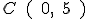 
y radio igual a 2 es
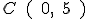y radio igual a 2 es
| |
| |
| |
|
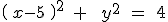
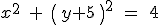
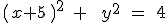
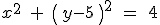
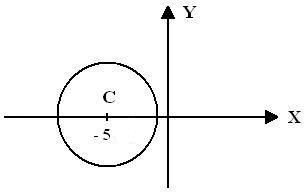
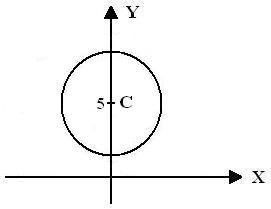
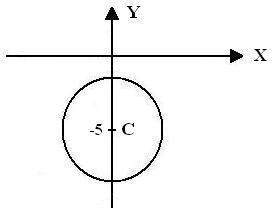
4.- La circunferencia de radio 2, cuyo centro 
es el punto de intersección entre las rectas 
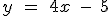y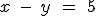 
, está representada gráficamente en la figura
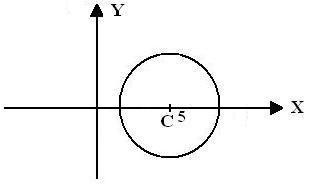
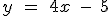es el punto de intersección entre las rectas y 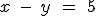, está representada gráficamente en la figura
| |
| |
| |
|
5.- Si uno de los extremos del diámetro de una circunferencia es el punto de coordenadas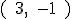 
y su centro se ubica en 
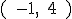entonces el radio es
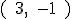y su centro se ubica en 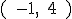entonces el radio es
| |
| |
| |
|
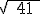
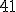
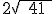
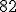
Hecho en México, todos los derechos
reservados 2008. Esta página puede ser reproducida con fines no lucrativos,
siempre y cuando no se mutile, se cite la fuente completa y su dirección
electrónica. De otra forma requiere permiso previo por escrito.
Facultad de Ingeniería-UNAM