|
PERIODO |
PERSONAJES |
CONTRIBUCIÓN |
|
Del
2000 al |
Utilizaron la escritura cuneiforme y
su legado escrito en tablillas de arcilla fue, entre otros aspectos: un
sistema de numeración posicional sexagesimal. Elaboraron tablas de
multiplicación, manejaron los quebrados. Poseen tablas de números cuadrados,
raíces cuadradas y cúbicas exactas. Llegaron a plantearse y resolver
ecuaciones hasta de tercer grado. Estos conocimientos produjeron un efecto
estimulante entre sus pueblos vecinos: egipcios, griegos e indios. |
|
|
Del
2000 al |
Se introduce el concepto de número
inverso, además de las soluciones a distintos problemas logarítmicos, e
incluso lograron la solución de sistemas de ecuaciones. Su avance fue tal que
crearon algoritmos para el cálculo de sumas de progresiones. |
|
|
Del
2000 al |
Los egipcios
inventaron el primer sistema de numeración, basado en la utilización de
jeroglíficos. |
|
|
Edad de oro de
las matemáticas griegas (época comprendida de los años 400 y |
(490 - |
Los sofismas
de Zenón constituyen la huella más vieja que se conserva del pensamiento
infinitesimal desarrollado muchos siglos después. |
|
(460- |
No se hicieron esperar los problemas
que implicaban el concepto de límites, por lo que, grandes pensadores como
Demócrito, intentan darles respuesta con la unificación de las matemáticas y
la teoría filosófica del atomismo. Considerando de esta forma la primera
concepción del método a límite. |
|
|
(408- |
Trabajó intensamente en la resolución
y demostración de distintos problemas, como en la trisección de un ángulo y
en la cuadratura de áreas acotadas por una curva. Esto conllevó al avance en
el cálculo del número
p y a la
creación del método de exhaución (predecesor del
cálculo de límites). |
|
|
(287 - |
Fue uno de los más
grandes pensadores de la antigüedad y uno de los matemáticos más originales
de todos los tiempos. Fue autor de innumerables inventos como el tornillo sin
fin, el engranaje con ruedas dentadas, el uso de la palanca en catapultas
militares, el espejo ustorio. Creo un
novedoso método teórico para el cálculo de áreas y volúmenes basado en
secciones infinitisimales. Estos trabajos fueron tomados por Newton y
Leibniz casi 2000 años después en el desarrollo del Cálculo. |
|
|
Alrededor del siglo
I d.C. |
Civilizaciones como |
Utilizaron un sistema
decimal jeroglífico, con la cualidad de que éstas implementaron el número
cero. |
|
A
partir del siglo VII |
Los Árabes |
Los avances obtenidos en esta época,
enmarcan al concepto de límite, la introducción de los números racionales e
irracionales, especialmente los reales positivos y el desarrollo en la
trigonometría, en donde se construyeron tablas trigonométricas de alta
exactitud. |
|
En el siglo XVII |
Matemático francés (1623-1662) Matemático inglés (1616-1703) Matemático francés (1602-1675) Matemático y físico francés (1596-1650) Matemático inglés (1630-1677) |
La aparición del análisis
infinitesimal fue la culminación de un largo proceso, cuya esencia matemática
interna consistió en la acumulación y asimilación teórica de los elementos
del cálculo diferencial e integral y la teoría de las series. Para el
desarrollo de este proceso se contaba con: el álgebra; las técnicas de
cálculo; introducción a las matemáticas variables; el método de coordenadas;
ideas infinitesimales clásicas, especialmente de Arquímedes; problemas de
cuadraturas; búsqueda de tangentes... Las causas que motivaron este proceso
fueron, en primer término, las exigencias de la mecánica, la astronomía y la
física. En la resolución de problemas de este género, en la búsqueda de
problemas generales de resolución y en la creación del análisis infinitesimal
tomaron parte muchos científicos. |
|
En
el año de 1601 |
Matemático alemán (1571-1630) |
En la esfera de las matemáticas, se
le atribuye el haber contribuido a crear el cálculo infinitesimal y estimular
el uso de los logaritmos en los cálculos. Fue uno de los primeros en advertir
el efecto que tiene la luna sobre las mareas. |
|
En el año de 1636 |
Abogado francés (1601—1665) |
Los primeros conceptos profundos en
el orden de lo infinitesimal se deben a estudios casi simultáneos de Fermat, Roberval y Torricelli, sobre todo a Fermat. Éste con su
estudio sobre las tangentes y sus trabajos sobre máximos y mínimos, problema
que abordó del mismo modo que se hace hoy día en el cálculo. Con esto se dijo
que Fermat es inventor del cálculo diferencial. Uno de los más grandes
matemáticos del siglo XVIII, Lagrange, así lo
aceptó. |
|
En
el año de 1638 |
Matemático italiano (1564--1642) |
En su obra Diálogos sobre dos nuevas ciencias
(movimiento y mecánica), inició la comprensión de estos temas, llevó a la
formulación de las leyes de movimiento de Newton, más precisas y al
perfeccionamiento que de esas leyes hicieron más tarde otros científicos. |
|
En
el siglo XVI |
Bonaventura
Francesco Cavalieri Matemático italiano (1598-1647) discípulo de Galileo. |
Cobra importancia por su teoría de
los “indivisibles”, que expuso en su obra “Geometria
indivisibilibus continuorum
quadam nova ratione promota”, publicada en 1965. Esta teoría estudia las
magnitudes geométricas como compuestas de un número infinito de elementos o
indivisibles. La medida de las longitudes, de las superficies y de los
volúmenes se convierte en la suma de la infinidad de indivisibles, el cual es
el principio del cálculo de una
integral definida, aunque sin la noción rigurosa de paso al límite.
Por esto puede ser considerado como uno de los precursores del análisis
infinitesimal moderno. |
|
En
el siglo XVI |
Matemático
italiano (1608-1647) discípulo de Galileo. |
Tempranamente hizo uso de los métodos
infinitesimales y determinó el punto en el plano de un triángulo, tal que la
suma de sus distancias de los vértices es la mínima (conocida como el centro isogónico). |
|
En
el año 1684 |
Matemático alemán (1646-1716) |
Nació en Leipzig,
Alemania; fue diplomático, jurista, lingüista, filósofo y matemático. Fue uno
de los grandes pensadores de los siglos XVII y XVIII y se le conoce como “El
último genio universal”. Empezó a estudiar matemáticas cuando tenía 26 años.
Realizó importantes contribuciones a la lógica simbólica, a la filosofía,
perfeccionó la máquina de calcular inventada por Pascal; pero su mayor fama
se debe a la invención, igual que Newton, del cálculo. en 1684, apareció la primera publicación sobre
cálculo diferencial: unas 7 páginas escritas por Leibniz en la revista
alemana Alta Eruditorum. Los últimos años de
la vida de Leibniz fueron amargados por la recia polémica que mantuvo con
Newton sobre la autoría de la invención del cálculo infinetesimal. |
|
En
el siglo XVII |
Matemático
inglés (1630-1677)
maestro de Newton. |
Barrow desarrolló un
método de determinación de tangentes que encierran aproximados métodos de
cálculo, fue el primero en establecer que la derivación y la integración son procesos
inversos. La conocida Regla de
Barrow fue llamada así en honor a él; sin embargo, también se le conoce como
la Regla de Newton-Leibniz o segundo Teorema fundamental del cálculo. |
|
En el año de 1687 |
Matemático inglés (1642-1727) |
Nació en Woolsthorpe
condado de Lincolnshire, Inglaterra el 25 de diciembre de 1642 según el
calendario juliano (4 de enero de 1643, según el calendario gregoriano). En 1664 la universidad de Cambridge
cerró sus puertas debido a una plaga que invadió la región y Newton volvió a
su pueblo natal, allí, en dos años de experimentos y reflexiones solitarias,
sentó las bases de sus grandes descubrimientos: la ley de la gravitación
universal, el cálculo infinitesimal, el teorema del binomio y la naturaleza
de la luz; tenía 23 años. Es curioso que Newton no hablara con
nadie de sus descubrimientos que fueron dados a conocer poco a poco, a veces
a 20 años después de su invención. Newton publica su invención del
cálculo infinitesimal en su obra monumental “Principia Matemática” en 1687, 3
años después que Leibniz. |
|
En el siglo XVII |
Matemático francés (1652-1719) |
Se dedicó esencialmente a la teoría
de ecuaciones donde obtuvo diversos resultados importantes, entre los que
destaca el reconocido teorema que lleva su nombre formulado en 1691. También inventó la notación
|
|
En el siglo XVII |
Matemático suizo (1654-1807) |
La familia Bernoulli, de Basilea,
Suiza, produjo 8 matemáticos importantes en 3 generaciones. El nombre de Johann Bernoulli está
relacionado con el marqués de L’ Hópital,
matemático aficionado, quien lo contrató como profesor. En 1696, L’ Hópital publicó, sin nombre de autor, el primer libro de
texto de cálculo infinitesimal. En ediciones posteriores figuraba el nombre
de L’ Hópital como autor. Posteriormente al haberse
encontrado correspondencia entre maestro y discípulo se supo que ese famoso
libro era una copia de las enseñanzas de Bernoulli. |
|
En el siglo XVIII |
Matemático inglés (1685-1731) Matemático escocés (1698-1746) |
Brook Taylor
publica en 1715 su obra “Los métodos de incrementación directa e inversa” en
ella agregaba a las matemáticas una nueva rama llamada “El cálculo de las
diferencias finitas”, el mismo trabajo contenía la célebre fórmula conocida
como la Serie de Taylor. Inventó la integración por partes e hizo otras
importantes contribuciones a la matemática. En 1742 Colin
MacLaurin publicó “Tratado de las fluxiones”, donde
introduce las llamadas Series de Maclaurin, caso
particular de las series de Taylor. Después de su muerte, en 1748 se publica
“Tratado de álgebra” donde usó determinantes para resolver sistemas de ecuaciones
con cuatro incógnitas. Dos años después este método fue popularizado por
Gabriel Cramer como Regla de Cramer.
|
|
En el siglo XVIII |
Matemático suizo (1707-1783) |
Alumno de J. Bernoulli. Sin duda
alguna el matemático más sobresaliente del siglo XVIII, a él se debe en gran
medida, después de Newton y Leibniz, el desarrollo del cálculo con la
publicación de su famoso libro “Introducción al análisis de las magnitudes
infinitamente pequeñas” en |
|
En los siglos XVIII - XIX |
Abogado francés (1717-1783) Matemático italiano (1736-1813) Matemático francés (1749-1827) Matemático alemán (1777-1855) |
Se postularon los fundamentos de las
matemáticas modernas. Avances en la resolución de ecuaciones. En cálculo,
hicieron de esta época la de mayor riqueza para esta parte de las
matemáticas. Entre los grandes desarrollos de esta época se puede
mencionar, la resolución de ecuaciones algebraicas radicales, el desarrollo
del concepto de grupo, avances en los fundamentos de la geometría hiperbólica
no euclidiana, además de la realización de una muy profunda reconstrucción
sobre la base de la creada teoría de límites, la teoría del número real y en
los problemas de optimización, el método de los multiplicadores de Lagrange. Se separaron y crearon varias ramas
de las matemáticas como ecuaciones diferenciales, la teoría de funciones de
variable real y la teoría de funciones de variable compleja. En relación con el análisis
matemático en este siglo, se fundamentó en un conjunto de procedimientos y
métodos de solución de numerosos problemas que crecía rápidamente. Todos
estos métodos aún podían dividirse en tres grandes grupos, constituidos en el
cálculo diferencial, el cálculo integral y la teoría de ecuaciones
diferenciales. Con estos fundamentos se llegó a lo que se conoce como teoría
de límites y de funciones, que fueron el tema central en este siglo. |
|
En el siglo XIX |
Matemático francés (1789-1857) |
Desarrolló la teoría de límites y
continuidad. Precisa los conceptos de función, límite y continuidad casi como
se manejan actualmente se deben a él. Dio bases sólidas al análisis infinitesimal
y fundamentó su uso. Definió los criterios de convergencia
y divergencia de las series. Fue el creador de la teoría de
funciones de variable compleja. |
|
En el siglo XIX |
Matemático checo (1781-1848) |
Fue el pionero
en el análisis de funciones, en sus trabajos estudió el criterio de
convergencia de sucesiones y dio una definición rigurosa de continuidad de
funciones. Estudió profundamente las propiedades de las funciones continuas y
demostró en relación con éstas una serie de notables teoremas, destacando el
denominado teorema de Bolzano: una función continua toma todos los valores
comprendidos entre su máximo y su mínimo. |
|
En el siglo XIX |
Matemático alemán (1804-1851) |
Autor muy prolífico,
contribuyó en varios campos de la matemática, principalmente en el área de
las funciones elípticas, el álgebra, la teoría de números y las ecuaciones
diferenciales. Una de sus obras más notables, publicada en 1841 fue “Sobre la
formación y propiedades de los determinantes”, en ella plantea la matriz jacobiana, el
determinante llamado jacobiano, así como una
de sus aplicaciones más interesantes, la determinación de los máximos y
mínimos para funciones de varias variables. |
|
En el siglo XIX |
Matemático inglés (1793-1841) Matemático y Físico irlandés (1819-1903) |
El teorema de Stokes
es llamado así en honor a George Gabriel Stokes, a pesar de que la primera
formulación conocida del teorema fue realizada por William Thomson y aparece
en una correspondencia que él mantuvo con Stokes fechada el 2 de julio de
1850. Stokes puso el teorema como una pregunta en el examen de 1854 del
premio de Smith, lo que dio como resultado que ahora lleve su nombre. El teorema de Green es
un caso particular del teorema de Stokes. |
|
En el siglo XIX |
Matemático alemán (1815-1897) |
Estableció las
definiciones de límite, continuidad y
derivada de una función como se usan hoy en día. Esto le permitió
demostrar un conjunto de teoremas que estaban entonces sin demostrar como el
teorema del valor medio y el teorema de Bolzano-Weierstrass. También realizó
aportaciones en convergencia de
series, en la teoría de funciones periódicas, convergencia de productos
infinitos, cálculo de variaciones y análisis complejo, entre otras
aportaciones en matemáticas. |
|
En el siglo XIX |
Matemático francés (1816-1900) Matemático francés (1819-1885) |
Jean Frenet en su tesis doctoral presentada en 1847 incluye la
teoría de curvas en el espacio, donde presenta las fórmulas que actualmente
son conocidas como “Fórmulas de Frenet-Serret”. Frenet aportó seis de dichas fórmulas, en tanto que Serret desarrolló las nueve restantes. Cabe señalar que Frenet publicó este apartado de su tesis en el “Journal de Mathématique pures et appliques”, en 1852. |
|
En el siglo XIX |
Matemático alemán (1826-1866) |
Realizó
contribuciones muy importantes al análisis y la geometría diferencial. Publica en 1854 su obra “Sobre la representación de una
función por una serie trigonométrica”, en ella se define por primera vez el
concepto de integral de Riemann y se inicia la teoría de funciones de una
variable real. |
Fue una antigua ciudad de la Baja Mesopotamia. Ganó su
independencia durante la Edad
Oscura, tras lo cual se convirtió en capital de un vasto imperio bajo el mandato de Hammurabi
(siglo XVIII a. C.).
Desde entonces se convirtió en un gran centro político, religioso y cultural.
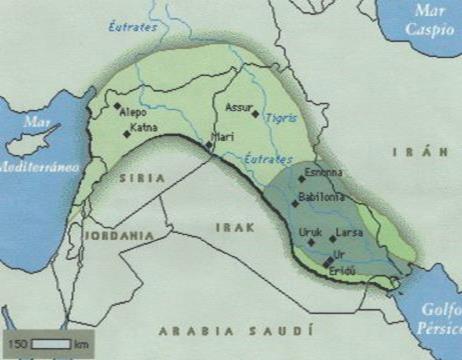
La civilización babilónica,
que duró desde el siglo XVIII hasta el VI a.C., era, como la sumeria que la
precedió, de carácter urbano, aunque se basaba en la agricultura más que en la
industria. El país estaba compuesto por unas doce ciudades, rodeadas de pueblos
y aldeas. A la cabeza de la estructura política estaba el rey, monarca absoluto
que ejercía el poder legislativo, judicial y ejecutivo. Por debajo de él había
un grupo de gobernadores y administradores selectos. Los alcaldes y los
consejos de ancianos de la ciudad se ocupaban de la administración local.
Los babilonios modificaron
y transformaron su herencia sumeria para adecuarla a su propia cultura y
carácter. El modo de vida resultante demostró ser tan eficaz que sufrió
relativamente pocos cambios durante aproximadamente 1 200 años. Influyó en sus
países vecinos, especialmente en el reino de Asiria, que adoptó la cultura
babilónica prácticamente por completo. Afortunadamente, se ha encontrado una
colección importante de obras de literatura babilónica gracias a las excavaciones.
Una de las más importantes es la magnífica colección de leyes (siglo XVIII
a.C.) frecuentemente denominada Código de Hammurabi, que, junto con otros
documentos y cartas pertenecientes a distintos periodos, proporcionan un amplio
cuadro de la estructura social y de la organización económica.
Los babilonios heredaron los logros
técnicos de los sumerios en riego y agricultura. El mantenimiento del sistema
de canales, diques, presas y depósitos construidos por sus predecesores
necesitaba de un considerable conocimiento y habilidad de ingeniería. La
preparación de mapas, informes y proyectos implicaban la utilización de
instrumentos de nivelación y jalones de medición. Con fines matemáticos y
aritméticos, utilizaban el sistema sexagesimal sumerio de numeración, que se
caracterizaba por un útil dispositivo denominado notación lugar-valor que se
parece al actual sistema decimal. Continuaron utilizándose las medidas de
longitud, área, capacidad y peso, normalizadas anteriormente por los sumerios.
La agricultura era una ocupación complicada y metódica que necesitaba
previsión, diligencia y destreza. Un documento escrito en sumerio recientemente
traducido, aunque utilizado como libro de texto en las escuelas babilónicas,
resulta ser un verdadero almanaque del agricultor, y registra una serie de
instrucciones y direcciones para guiar las actividades de la granja, desde el
riego de los campos hasta el aventamiento de los cultivos cosechados.
Los artesanos babilonios eran diestros en
metalurgia, en los procesos de abatanado, blanqueo y tinte, y en la preparación
de pinturas, pigmentos, cosméticos y perfumes. En el campo de la medicina, se
conocía bien la cirugía y se practicaba frecuentemente, a juzgar por el Código
de Hammurabi, que la dedica varios párrafos. También se desarrolló, sin lugar a
dudas, la farmacopea, aunque la única prueba importante de ello procede de una
tablilla sumeria escrita algunos siglos antes del reinado de Hammurabi.
Más de 1.200 años pasaron
desde el glorioso reinado de Hammurabi hasta la subyugación de Babilonia por
los persas. Durante este largo lapso de tiempo, la estructura social, la
organización económica, el arte y la arquitectura, la ciencia y la literatura,
el sistema judicial y las creencias religiosas babilónicas sufrieron una
considerable modificación, aunque en general únicamente en los detalles, no en
la esencia. Basados prácticamente por completo en la cultura de Sumer, los
logros culturales de Babilonia dejaron una profunda impresión en el mundo
antiguo, y particularmente entre los hebreos y los griegos. La influencia
babilónica es evidente en las obras de poetas griegos tales como Homero y
Hesíodo, en la geometría del matemático griego Euclides, en astronomía, en
astrología, en heráldica y en la Biblia.
No podemos dejar de mencionar a los Jardines
Colgantes de Babilonia, una de las 7 maravilla
de la Antigüedad, que fueron mandados construir por Nabucodonosor II para su esposa Amytis,
procedente del norte de Media
(Oriente Medio), que añoraba su tierra montañosa y verde, ocupaban un lugar
entre el río Éufrates y la Avenida
de las Procesiones, ligados al gran palacio de Nabucodonosor. Aunque se han
teorizado diversos modelos arquitectónicos de su construcción, aún se desconoce
el sistema exacto utilizado para su creación; se han encontrado sin embargo
poleas y diversos restos de, quizá, un sistema hidráulico, que permiten
situarlos en ese lugar, además de restos de arcos construidos en piedra,
material extraño en una ciudad donde casi todas las construcciones son de
adobe, que elevaban el suelo unos 20 metros.

Reconstrucción artística de Babilonia, con los Jardines Colgantes
en primer plano, efectuada en un cuadro del pintor del siglo XVI Martin Heemskerck.
Los jardines estaban junto al palacio del Rey, contiguo al río,
para que los viajeros los pudieran contemplar, ya que el acceso al pueblo estaba prohibido. En la más alta de
las terrazas se situaba un depósito de agua desde el cual corrían varios arroyos.
Los Jardines Colgantes de Babilonia no "colgaban" realmente en
el sentido de estar suspendidos por cables o cuerdas. El nombre proviene de una
traducción incorrecta de la palabra griega kremastos o del término en latín pensilis,
que significa no justamente "colgar" pero si "sobresalir",
como en el caso de una terraza o de un balcón.
El geógrafo griego Estrabón, quien describió los jardines en el siglo I a. C., escribió:
“Éste consta de terrazas abovedadas alzadas unas sobre otras, que
descansan sobre pilares cúbicos. Éstas son ahuecadas y rellenas con tierra para
permitir la plantación de árboles de gran tamaño. Los pilares, las bóvedas, y
las terrazas están construidas con ladrillo cocido y asfalto.”
Las excavaciones arqueológicas más recientes en la antigua ciudad
de Babilonia, en el actual territorio de Irak destaparon el asentamiento del
palacio. Otros hallazgos incluyen la construcción abovedada con paredes gruesas
y una irrigación cerca del palacio meridional.
MESOPOTAMIA
Mesopotamia (en griego
significa “entre ríos”), región que se convirtió en uno de los
primeros centros de civilización urbana, situada entre los ríos Tigris y
Éufrates, en la zona que en la actualidad ocupan los estados de Irak
(principalmente), Irán y Siria.
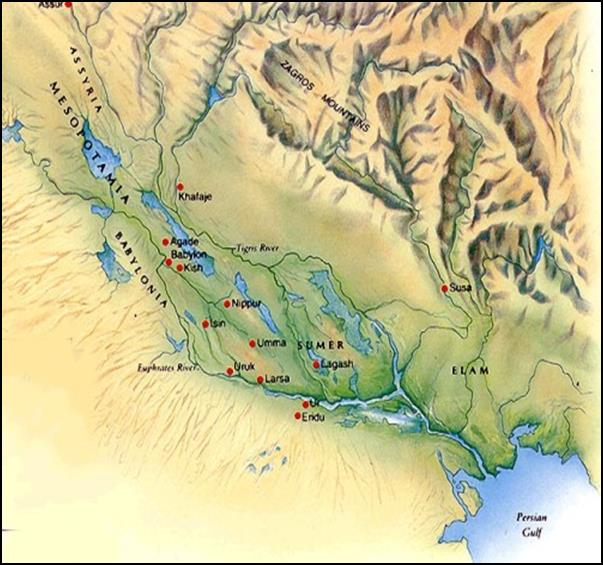
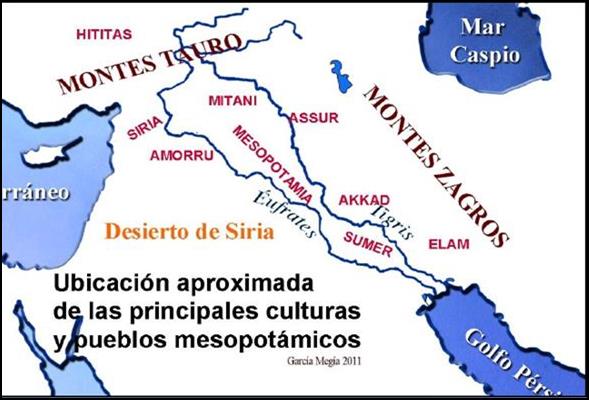
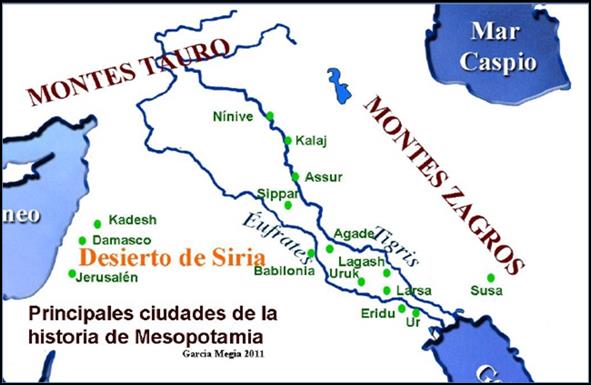
La riqueza natural de
Mesopotamia siempre ha atraído a pueblos procedentes de las regiones vecinas
más pobres, y su historia es la de continuas migraciones e invasiones. La
lluvia es escasa en la mayor parte de la región, pero cuando el fértil suelo se
riega a través de canales produce abundantes cultivos.
La necesidad de autodefensa
y riego llevó a los antiguos mesopotámicos a organizar y construir canales y
asentamientos fortificados. Desde el 6000 a.C. los asentamientos
aumentaron, convirtiéndose en ciudades en el IV milenio a.C. El primer asentamiento
de la región fue probablemente Eridú, aunque el
ejemplo más destacado es Uruk (la Erech bíblica) al
sur, donde los templos de adobe se decoraron con fina metalurgia y piedras
labradas. El desarrollo de una administración también estimuló la invención de
una forma de escritura, la cuneiforme. Los sumerios probablemente fueron
responsables de esta primera cultura urbana que se extendió hacia el norte del
Éufrates. Otros asentamientos importantes de Sumer fueron Adab,
Isin, Kis, Larsa, Nippur y Ur.
Hacia el 2330 a.C. la
región fue conquistada por los acadios, pueblo semítico del centro de
Mesopotamia. Su rey, Sargón I el Grande (que reinó hacia el
2335-2279 a.C.), fundó la dinastía de Acad, y en
su época la lengua acadia comenzó a sustituir al sumerio. Los gutis, tribu de las colinas del este, acabaron con el
dominio acadio hacia el 2218 a.C., y, después de un intervalo, la III
Dinastía de Ur llegó a dominar gran parte de
Mesopotamia. En Ur, hubo un florecimiento final de
las tradiciones sumerias. Los invasores precedentes del reino norteño de Elam destruyeron la ciudad de Ur
hacia el 2000 a.C. Bajo su dominio ninguna ciudad consiguió el control
total hasta mediados del siglo XVIII, cuando Hammurabi de Babilonia unificó el
país durante algunos años al final de su reinado. Al mismo tiempo, una familia
amorrea obtuvo el control de Assur en el norte; sin
embargo, tanto Babilonia como Assur pronto cayeron a
manos de los recién llegados. Hacia el 1595 a.C. los hititas tomaron
Babilonia que poco después cayó bajo el control de los casitas. Durante los 400
años siguientes Babilonia se desarrolló notablemente; sus reyes adquirieron un
poder similar al de los faraones de Egipto y su población estableció amplias
relaciones comerciales. Assur cayó en manos del reino
de Mitanni, fortalecido por los hurritas
procedentes del Cáucaso, quienes probablemente estaban relacionados con el
pueblo de Urartu. Los hurritas
habían estado en Mesopotamia durante siglos, pero después del 1700 a.C. se
extendieron por todo el norte y también por Anatolia.
Hacia el 1350 a.C., el
reino de Asiria, al norte de Mesopotamia, comenzó a destacar. El ejército
asirio derrotó a Mitanni, conquistando en poco tiempo
Babilonia hacia el 1225 a.C., y llegando al Mediterráneo hacia el
1100 a.C. Durante los dos siglos siguientes, esta expansión fue detenida
por las tribus arameas procedentes de la estepa siria y, con la ayuda de tribus
caldeas, invadieron Babilonia. Asiria combatió a éstas y a otras tribus,
expandiéndose de nuevo después del 910 a.C. Durante su mayor extensión
(c. 730-650 a.C.) el Imperio asirio controló Oriente Próximo desde
Egipto hasta el golfo Pérsico. Las regiones conquistadas quedaron bajo el mando
de reyes vasallos o, si existían problemas, eran anexionadas. Siguiendo una antigua
práctica, los individuos rebeldes eran deportados, produciéndose una mezcla de
razas en todo el Imperio. Las frecuentes revueltas precisaban una fuerte
potencia militar, pero no se pudo mantener el control en un dominio tan amplio
durante mucho tiempo. Las presiones internas y los ataques de los pueblos de
Media y los caldeos de Babilonia provocaron el colapso en el 612 a.C. Los
medos tomaron la parte elevada del país, dejando Mesopotamia a los caldeos bajo
el gobierno de Nabucodonosor II. Los caldeos rigieron Mesopotamia hasta el
539 a.C., cuando Ciro el Grande de Persia, quien había conquistado Media,
capturó Babilonia.
Bajo los persas, Mesopotamia
se dividió en las satrapías (provincias) de Babilonia y Assur,
desempeñando Babilonia un papel fundamental en el Imperio. La lengua aramea,
ampliamente hablada con anterioridad, se convirtió en el idioma común, y el
establecimiento de un gobierno imperial trajo consigo la estabilidad a la
región. Sin embargo, al final, el régimen fue demasiado opresivo y la prosperidad
de Mesopotamia declinó.
Las culturas de Mesopotamia fueron pioneras en
muchas de las ramas de conocimiento; desarrollaron la escritura que se denominó
cuneiforme, en principio pictográfica y más adelante la fonética; en el campo
del derecho, crearon los primeros códigos de leyes; en arquitectura,
desarrollaron importantes avances como la bóveda y la cúpula, crearon un
calendario de 12 meses y 360 días e inventaron el sistema de numeración sexagesimal.
Sus restos, aunque quizás todavía hay muchos por
descubrir, muestran una cultura que ejerció una poderosa influencia en otras
civilizaciones del momento y por ende el desarrollo de la cultura occidental.
El cálculo floreció en Mesopotamia mediante un
sistema de numeración decimal y sistema sexagesimal, cuya primera aplicación
fue en el comercio. Además de la suma y resta conocían la multiplicación y la
división y, a partir del II milenio a. C. desarrollaron una
matemática que permitía resolver ecuaciones hasta de tercer grado. Conocían
asimismo un valor aproximado del número π, de la raíz y la potencia, y
eran capaces de calcular volúmenes y superficies de las principales figuras
geométricas.
La
astronomía floreció de igual forma. Los sumerios sabían distinguir entre
planetas –objetos móviles– y estrellas. Pero fueron los babilonios quienes más
desarrollaron este campo, siendo capaces de prever fenómenos astronómicos con
antelación. Este conocimiento de la astronomía les llevó a adoptar un preciso
calendario lunar, que incluía un mes suplementario que lo ajustaba al solar.
También se han encontrado tratados de medicina y
listados sobre geología, en los que se trataba de clasificar los diferentes
materiales.
LOS EGIPCIOS
Antiguo
Egipto, periodo de la historia de Egipto que abarca desde
su protohistoria hasta el siglo VII d.C., y que comprende, por tanto, el
conjunto de su edad antigua y parte de su edad media.
La antigua civilización egipcia fue
notable no solo por la riqueza, esplendor y sofisticación de su arquitectura
funeraria, que refleja y atestigua el poder de sus faraones y la habilidad de
sus ingenieros. También lo fue por su desarrollado sistema de gobierno; por la
aplicación de sistemas de irrigación; por su escritura pictográfica; por sus
estudios en los campos de la astronomía, las matemáticas y la medicina; por la
creación de una cultura espiritual muy compleja, patente en sus panteones y en
sus conceptos de vida ultraterrena; así como por su destreza y sensibilidad
artísticas.
La misteriosa Esfinge, con cuerpo de león y cabeza
humana, y la perfecta simetría de las pirámides de Gizeh
son símbolos mundialmente conocidos del antiguo Egipto. La más antigua de las
tres pirámides se construyó alrededor del 2600 a.C. Todas tienen cámaras
funerarias. La imponente estatua de la Esfinge se construyó con gigantescos
bloques de caliza hace más de 4.000 años.

Las cámaras sepulcrales de las pirámides egipcias
albergaban el sarcófago del faraón y los bienes materiales que debían
acompañarle en su viaje al más allá. Estas cámaras estaban situadas al final de
largos pasajes que podían estar sellados o construidos de forma que
confundieran a los posibles ladrones de tumbas. Esta sección transversal de la
pirámide de Keops muestra la disposición interna del conjunto de pasajes y cámaras
sepulcrales.
Los antiguos egipcios utilizaban su lengua escrita
para los textos religiosos, pero, por su naturaleza pictórica, los jeroglíficos
también fueron un popular elemento decorativo en las estatuas, como la de la
imagen.
En 1799 cerca de Rosetta, una ciudad egipcia, el Ejército francés encontró la piedra de Rosetta que fue la clave para descifrar la escritura jeroglífica del antiguo Egipto. Esta piedra de basalto negro fue grabada hacia el 196 a.C. con tres inscripciones de idéntico contenido en honor al rey Tolomeo V, pero con tres alfabetos diferentes: el jeroglífico, el demótico y el griego. Al comparar las tres versiones, los investigadores lograron desentrañar el significado de los jeroglíficos, y así sentaron las bases de la egiptología.
El conocimiento que en la actualidad
se tiene del antiguo Egipto se debe, en buena parte, a los grandes monumentos
que aquella civilización legó; y a la arqueología, que los descubrió, analizó y
estudió. Una significativa faceta de la egiptología (que se define como el
estudio de la civilización del antiguo Egipto) es la investigación de la
valiosísima información proporcionada por los textos escritos en caracteres
jeroglíficos que se han hallado en las paredes y muros de tumbas y templos, en
obeliscos y columnas, y en tablillas de arcilla y papiros. La interpretación de
esos jeroglíficos, que fue posible gracias al hallazgo, en 1799, de la piedra
de Rosetta, ha permitido conocer progresivamente
múltiples aspectos de la vida del antiguo Egipto. Otra fuente que resultó
fundamental para la reconstrucción de su historia fue el Aegyptiaca
de Manetón, un sacerdote tolemaico del siglo
III a.C. que organizó una lista de reyes dividida en 30 dinastías.
PRIEDRA ROSETA

Ciencia
La ciencia del antiguo Egipto gozó de gran prestigio desde
tiempos remotos. Es enormemente significativo el alto nivel que desarrolló esta
civilización y la amplitud de conocimientos que sus escribas habían llegado a
dominar. La tradición refleja que los hombres sabios de la antigua Grecia iban
a aprender a Egipto, en donde existía una ciencia venerable y un elevado nivel
de conocimientos científicos, aunque algunas veces mezclados con prácticas
mágicas.
Matemáticas
Entre todas las ramas de la ciencia que desarrollaron, la
que más avanzaron fueron las matemáticas. La necesidad de volver a marcar los
límites de los terrenos al bajar el nivel del agua del Nilo, tras de las
inundaciones anuales, impulsó el desarrollo de la geometría y los instrumentos
de medición, tanto del terreno como del tiempo, que fueron bastante precisos.
Papiro de Rhind
El Papiro de Ahmes, también conocido como Papiro Rhind,
es un documento de carácter didáctico que contiene diversos problemas
matemáticos. Está redactado en escritura hierática y mide unos seis metros de
longitud por 32 cm de anchura. Se encuentra en buen estado de conservación. El
texto, escrito durante el reinado de Apofis I, es
copia de un documento del siglo XIX a. C. de época de Amenemhat
III.
Fue
escrito por el escriba Ahmes a mediados del siglo XVI
a. C., a partir de textos de trescientos años de antigüedad, según relata Ahmes al principio del texto.
El
papiro fue encontrado en el siglo XIX, junto a un rollo de cuero, entre las
ruinas de una edificación próxima al Ramesseum, y
adquirido por Henry Rhind en 1858. Dos fragmentos se
custodian desde 1865 en el Museo Británico de Londres (EA 10057-8), aunque no
están expuestos al público.
Contiene
87 problemas matemáticos con cuestiones aritméticas básicas, fracciones,
cálculo de áreas, volúmenes, progresiones, repartos proporcionales, regla de
tres, ecuaciones lineales y trigonometría básica.
Su contenido puede clasificarse en:
Operaciones con números racionales enteros y fraccionarios
(1 a 23, 47, 80, 81);
Resolución de ecuaciones de primer grado (24 a 27, 30 a
38);
Problemas de "pensar un número..." (28, 29);
Progresiones aritméticas (39, 40 y 64);
Volúmenes, capacidades y poliedros (41 a 46, 56 a 60);
Áreas de figuras planas (48 a 55);
Regla para obtener los 2/3 de números pares (61 y 61B);
Proporciones (62, 63, 65 a 68);
Progresiones geométricas (79);
Varios (80 a 87).
En él encontramos el tratamiento de las fracciones. Los
antiguos egipcios no realizaban el cálculo de fracciones como lo conocemos hoy,
pues escribían los números fraccionarios como suma de fracciones unitarias (las
de la forma 1/n con n natural) distintas. Este tipo de sumas son conocidas hoy
como fracciones egipcias.
PAPIRO DE RHIND

ZENÓN DE
ELEA

Fue un filósofo griego nacido en Elea,
al suroeste de Italia (490-430 a. C.), perteneciente a la escuela eleática discípulo
directo de Parménides de
Elea, llegó
a ser su discípulo predilecto y le acompañó a Atenas cuando tenía 40 años.
Como sucede con la mayoría de los filósofos presocráticos, la vida de Zenón de
Elea permanece en gran parte desconocida. Las fuentes que brindan luz al
respecto son el diálogo Parménides de Platón y la obra Vida de los filósofos ilustres del historiador y filósofo antiguo Diógenes Laercio.
En el diálogo de Platón, se dice que Zenón tiene cerca de 40 años
y que Parménides roza los 65 en el momento en que ambos se encuentran con un Sócrates "muy joven". Platón lo
describe como "alto y bello a la mirada", así como estimado por su
maestro.
Diógenes Laercio indica que fue hijo
natural de un hombre llamado Telentágoras, pero que
Parménides lo tomó en adopción. Laercio subraya así
mismo su destreza a la hora de analizar los dos lados de cada cuestión o
dilema, capacidad que le hizo recibir el título de "inventor de la dialéctica" de la mano de Aristóteles.
En Atenas, Zenón enseñó filosofía durante algunos
años, concentrándose en el sistema eleático de metafísica. El estadista
ateniense Pericles y Calias estudiaron con él. Zenón
regresó más tarde a Elea y, según cuenta la tradición, se unió a una
conspiración para librar a su ciudad nativa del tirano Nearcco;
la conspiración fracasó y Zenón fue torturado con dureza, pero se negó a
delatar a sus compañeros. No se conocen más circunstancias de su vida.
Sólo pocos fragmentos de la obra de Zenón perduran,
pero las obras de Platón y Aristóteles se nutren de referencias textuales de
los escritos de Zenón. En el plano filosófico, Zenón aceptaba la creencia de
Parménides de que el universo, o el ser, es una sustancia indiferenciada, simple,
única, aunque pueda parecer diversificada para los sentidos. La intención de
Zenón fue desacreditar las sensaciones, lo que pretendió hacer a través de una
brillante serie de argumentos o paradojas, sobre el espacio y el tiempo que han
perdurado hasta nuestros días como mosaicos intelectuales complejos. Una
paradoja clásica afirma que un corredor no puede llegar a la meta porque, para
lograrlo, debe recorrer una distancia; pero no puede recorrer esa distancia sin
primero recorrer la mitad de ella, y así ad infinitum. Porque existe un
número infinito de bisecciones en una distancia espacial, uno no puede recorrer
una distancia en tiempo finito, a menos que acorte la distancia o aumente la
velocidad. Este argumento, como muchos otros de Zenón, se proponía demostrar la
imposibilidad lógica del movimiento. Dado que los sentidos nos llevan a creer
en la existencia del movimiento, los sentidos son ilusorios y por lo tanto no
existe ningún obstáculo para aceptar las inverosímiles teorías de Parménides de
otra forma. Zenón es reconocido no sólo por sus paradojas, sino por establecer
los debates filosóficos que favorecen la discusión razonada. Por todo ello,
Aristóteles le consideró el creador del razonamiento dialéctico.
Se le ha considerado el primero en utilizar la demostración
llamada ad absurdum (reducción al absurdo), que toma por hipótesis lo contrario de lo que se considera
cierto y muestra las incongruencias que se derivan de una consideración de esto
como verdadero, obligando al
interlocutor a rechazar las premisas y a aceptar las tesis opuestas, que eran las que se querían
demostrar en un principio. Este procedimiento lo lleva a cabo mediante sus
aporías.
Los razonamientos de Zenón constituyen el testimonio más antiguo
que se conserva del pensamiento infinitesimal desarrollado muchos siglos después en
la aplicación del cálculo
infinitesimal que nacerá de la mano de Leibniz y Newton en 1666.
No obstante, Zenón era ajeno a toda posible matematización,
presentando una conceptualización de tal estilo como un instrumento necesario
para poder formular sus paradojas.

Fue un filósofo griego (460-370
a. C.), que desarrolló la teoría atómica del universo, concebida por su mentor,
el filósofo Leucipo. Demócrito, cuyo nombre significa
"escogido del pueblo", conocido por el sobrenombre de Milesio o Abderita nació en Abdera, Tracia.
Escribió numerosas obras, pero sólo perduran escasos fragmentos de ellas.
Se le considera un filósofo
presocrático tradicionalmente,
aunque es un error de cronología, ya que fue contemporáneo de Sócrates y también es un error desde el punto
de vista filosófico: la mayor parte de sus obras tratan de ética y apenas nada
de physis, cuyo estudio
caracterizaba a los presocráticos.
Demócrito fue discípulo y después sucesor de Leucipo de Mileto, natural también de Abdera. Fueron además oriundos de Abdera: Anaxarco y Protágoras.
Demócrito de Abdera fue conocido en su
época por su carácter extravagante. Se le adjudican numerosas leyendas. Realizó
muchos viajes por Egipto, Persia y Mesopotamia, donde habría aprendido de magos
persas, sacerdotes egipcios y caldeos. Se dice de él que presentía lo futuro y
entre sus obras más importantes se cita su "Gran Diacosmos",
por la cual obtuvo, por plebiscito popular, el premio de 500 talentos. Demócrito murió a los 90 años de edad,
aunque todos los autores de la antigüedad que hayan hecho referencia a su edad,
coinciden en que vivió más de cien años.
Según
la teoría atómica de la materia de Demócrito, todas las cosas están compuestas
de partículas diminutas, invisibles e indestructibles de materia pura (en
griego atoma, 'indivisible'), que se mueven
por la eternidad en un infinito espacio vacío (en griego kenon,
'el vacío'). Aunque los átomos estén hechos de la misma materia, difieren en
forma, medida, peso, secuencia y posición. Las diferencias cualitativas en lo
que los sentidos perciben y el origen, el deterioro y la desaparición de las
cosas son el resultado no de las características inherentes a los átomos, sino
de las disposiciones cuantitativas de los mismos. Demócrito consideraba la
creación de mundos como la consecuencia natural del incesante movimiento
giratorio de los átomos en el espacio. Los átomos chocan y giran, formando
grandes agregaciones de materia. Muchos consideran
que Demócrito es "el padre de la ciencia moderna".
Demócrito escribió también sobre ética, proponiendo
la felicidad, o 'alegría', como el mayor bien —una condición que se logra a
través de la moderación, la tranquilidad y la liberación de los miedos. En la
historia Demócrito era conocido como el Filósofo Alegre, en contraste al más
sombrío y pesimista Heráclito. Su teoría atómica anticipó los modernos
principios de la conservación de la energía y la irreductibilidad de la materia.
Se dice que viajó por Egipto,
donde vivió cinco años y adquirió conocimientos de geometría; visitó Etiopía,
Mesopotamia, Babilonia, Caldea y Persia y
que incluso llegó a la India en busca de conocimientos. Había
adquirido dinero para viajar de la herencia que le dejó su padre a él y a sus
dos hermanos; le correspondieron cien talentos.
Siendo ampliamente ignorado en Atenas durante su vida, la obra de Demócrito
fue bastante conocida por Aristóteles,
que la comentó extensamente. Es famosa la anécdota que Platón detestaba tanto a Demócrito que
quería que todos sus libros fuesen quemados. Se
dice que estuvo a punto de quemarlos pero que se lo impidieron los pitagóricos Amiclas y Clitias aludiendo que era
inútil pues ya sus escritos circulaban en muchas partes.
Diógenes Laercio listó una serie de escritos de
Demócrito que superan las 70 obras sobre ética, física, matemática, técnica e
incluso música, por lo que Demócrito es considerado un autor enciclopédico. No
se conservaron tales escritos, de toda esta producción sólo nos quedan unos
trescientos fragmentos menores, la mayor parte de los cuales son reflexiones
morales de las cuales sólo conocemos fragmentos, sobre todo gracias a las
alusiones de Aristóteles y de Teofrasto.
Existen diversas colecciones de esos fragmentos, como las de Diels-Kranz, Luria y Leszl.

Eudoxo
(408-355 a.C.), astrónomo y matemático griego que realizó importantes
aportaciones en el campo de la geometría y expuso la primera explicación
sistemática de los movimientos del Sol, la Luna y los planetas. Eudoxo nació en Cnido (en lo que
actualmente es Turquía). Fue discípulo del filósofo Arquitas y estudió con
Platón durante un breve periodo.
A Eudoxo se le atribuye generalmente el descubrimiento de que
el año solar tiene 6 horas más de los 365 días. Eudoxo
también intentó explicar los movimientos del Sol, la Luna y los planetas
mediante un modelo del Sistema Solar basado en una complicada combinación de
esferas que giran. Su modelo tuvo un relativo éxito en la predicción de estos
movimientos. Eudoxo también llevó a cabo importantes
descubrimientos en matemáticas; se le atribuyen muchos en geometría,
posteriormente incluidos en los Elementos de Euclides.
Fue discípulo
de Arquitas de Tarento. Su trabajo sobre la teoría de la proporción denota una
amplia comprensión de los números y permite el tratamiento de las cantidades
continuas, no únicamente de los números enteros o números racionales. Cuando
esta teoría fue resucitada por Tartaglia y otros
estudiosos en el siglo XVI, se convirtió en la base de muchas obras de ciencias
durante un siglo, hasta que fue sustituida por los métodos algebraicos de
Descartes.
Eudoxo
demostró que el volumen de una pirámide es la tercera parte del de un prisma de
su misma base y altura; y que el volumen de un cono es la tercera parte del de
un cilindro de su misma base y altura, teoremas ya intuidos por Demócrito. Para
demostrarlo elaboró el llamado método de exhausción,
antecedente del cálculo integral, para calcular áreas y volúmenes. El método
fue utilizado magistralmente por Arquímedes. El trabajo de ambos como
precursores del cálculo fue únicamente superado en sofisticación y rigor
matemático por Newton y Leibniz.

Arquímedes (287-212 a.C.), notable matemático e inventor
griego, que escribió importantes obras sobre geometría plana y del espacio,
aritmética y mecánica.
Nació en Siracusa, Sicilia, y se educó en Alejandría,
Egipto. En el campo de las matemáticas puras, se anticipó a muchos de los
descubrimientos de la ciencia moderna, como el cálculo integral, con sus
estudios de áreas y volúmenes de figuras sólidas curvadas y de áreas de figuras
planas. Demostró también que el volumen de una esfera es dos tercios del
volumen del cilindro que la circunscribe. Pidió a sus amigos y parientes que,
cuando muriera, esculpieran sobre la losa de su tumba una esfera inscrita
dentro de un cilindro, siendo el volumen del cilindro igual a 1,5 veces el volumen
de la esfera.
Se considera que Arquímedes fue uno de los matemáticos más
grandes de la antigüedad y, en general, de toda la historia. Usó el método
exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio
de una serie infinita, y dio una aproximación extremadamente precisa del número
![]() .
También demostró que el área del círculo era igual a
.
También demostró que el área del círculo era igual a ![]() multiplicado por el cuadrado del radio del
círculo. Definió fórmulas para los volúmenes de las superficies de revolución y
un ingenioso sistema para expresar números muy largos.
multiplicado por el cuadrado del radio del
círculo. Definió fórmulas para los volúmenes de las superficies de revolución y
un ingenioso sistema para expresar números muy largos.
En mecánica, Arquímedes definió la ley de la palanca y se
le reconoce como el inventor de la polea compuesta. Durante su estancia en
Egipto inventó el “tornillo sin fin” para elevar el agua de nivel, sacándola de
un río. Arquímedes es conocido sobre todo por el descubrimiento de la ley
fundamental de la hidrostática, el llamado principio de Arquímedes, que
establece que todo cuerpo sumergido en un fluido experimenta una pérdida de
peso igual al peso del volumen del fluido que desaloja. Se dice que este
descubrimiento lo hizo mientras se bañaba, al comprobar cómo el agua se
desplazaba y se desbordaba; sorprendido por su hallazgo saltó fuera de la
bañera, y corrió por las calles de Siracusa gritando: “¡Eureka!, ¡Eureka!”, que
significa “lo encontré”. Aplicando este principio comprobó que la corona de oro
que había mandado fabricar su protector, el rey Hierón,
no tenía la misma densidad que el oro puro, por lo que supo que el orfebre le
había engañado, no había utilizado solamente el oro que el rey le había
proporcionado.
Arquímedes pasó la mayor parte de su vida en Sicilia, en
Siracusa y sus alrededores, dedicado a la investigación y los experimentos.
Aunque no tuvo ningún cargo público, durante la conquista de Sicilia por los
romanos se puso a disposición de las autoridades de la ciudad y muchos de sus
instrumentos mecánicos se utilizaron en la defensa de Siracusa. Entre la
maquinaria de guerra cuya invención se le atribuye está la catapulta y un
sistema de espejos —quizá legendario— que incendiaba las embarcaciones enemigas
al enfocarlas con los rayos del sol.
Al ser conquistada Siracusa, durante la segunda Guerra
Púnica, fue asesinado por un soldado romano que le encontró dibujando un
diagrama matemático en la arena. Se cuenta que Arquímedes estaba tan absorto en
las operaciones que ofendió al intruso al decirle: “No desordenes mis
diagramas”. En un mosaico hallado en las ruinas de Herculano
aparece representada esta escena.
Todavía subsisten muchas de sus obras sobre matemáticas y
mecánica, como el Tratado de los cuerpos flotantes, El arenario
y Sobre la esfera y el cilindro. Todas ellas muestran el rigor y la imaginación
de su pensamiento matemático.

Blaise Pascal (1623-1662) fue matemático,
físico, filósofo cristiano y escritor francés. Sus contribuciones a las matemáticas y las ciencias
naturales incluyen el diseño y construcción de calculadoras mecánicas, aportes a la Teoría
de la probabilidad, investigaciones sobre los fluidos y la aclaración de conceptos tales como la presión y el vacío. Después de una experiencia religiosa profunda en 1654,
Pascal abandonó las matemáticas y la física para dedicarse a la filosofía y a la teología. Considerado
una de las mentes privilegiadas de la historia intelectual de Occidente.
Blaise Pascal nació en el seno de una familia noble en Clermont (hoy en día Clermont-Ferrand). Su padre, Étienne
Pascal, tras haber recibido una formación como jurista en París, era un magistrado de alto rango
que se desempeñaba como juez vicepresidente de la oficina de recaudación
tributaria de Auvernia en Clermont. Por otra parte, Étienne
Pascal destacaría más tarde como matemático. Su madre, Antoinette
Begon provenía de una familia burguesa de
comerciantes acomodados. Blaise Pascal tenía dos hermanas, Gilberte
y Jaqueline. A la primera, tres años mayor que Blaise, se le conoce mucho más,
puesto que fue ella quien escribió la primera biografía publicada sobre su
hermano. Al nacer Jaqueline, su hermana dos años menor, la madre no logró
recuperarse de aquel parto complicado y el puerperio, de modo que Pascal perdió
su madre a la temprana edad de tres años.
En 1631, Étienne Pascal se trasladó con
su familia a París, conservando en Clermont su puesto en la oficina de
recaudación de impuestos. También llevó a una niñera que estaba a cargo del
cuidado de sus tres hijos huérfanos de madre. Blaise
tenía para entonces ocho años y el objetivo de su padre era abrirle en la
capital francesa mayores posibilidades que las existentes en la provincia para
su educación y despliegue de capacidades, a todos los hijos, pero
particularmente para Blaise, quien llamaba mucho la atención por su capacidad
intelectual superdotada.
Resulta sorprendente que Pascal no haga ninguna mención de esta
temprana pérdida. Al respecto, su hermana Gilberte
Pascal escribirá en la biografía:
...al morir mi madre en 1626, cuando mi hermano no tenía más que
tres años, mi padre, al quedarse solo, se entregó con mayor dedicación al
cuidado de la familia; y como Blaise era su único hijo varón, esta cualidad y
las demás que en él observó (las grandes pruebas de inteligencia que observó en
él) le llenó hasta tal punto de afecto paternal que decidió no encargar a nadie
la tarea de su educación y tomó la resolución de instruirle él mismo, como en
efecto hizo, pues mi hermano no tuvo nunca otro maestro que mi padre...
En 1640, su padre fue nombrado Comisario Real
y jefe de la recaudación de impuestos para Normandía con asiento en Ruan. Aquí, en 1642, Pascal inventó
para él la “rueda de pascal” o “Pascalina”,
considerada como una de las calculadoras más antiguas. Inicialmente solo
permitía realizar adiciones, pero en el curso de los diez años siguientes
añadió mejoras, siendo finalmente capaz de hacer restas. Pascal la hizo
patentar, pero no se cumplieron sus expectativas de hacerse rico
comercializando su invento por medio de una pequeña empresa de su propiedad.
Las máquinas, trabajosamente confeccionadas una a una y a mano, eran demasiado
caras como para poder venderse en volúmenes mayores y solo llegó a fabricar
cincuenta, de las que subsisten nueve.

Pascalina
En 1646, durante la convalecencia del padre después de un
accidente, la familia, que hasta entonces no había sido muy religiosa, entró en
contacto con las enseñanzas del obispo reformista holandés Jansenio,
que defendía en el seno de la iglesia católica una noción de gracia divina basada en San Agustín, similar a las ideas de Calvino. El padre, el hijo y las hijas
se hicieron devotos y Jacqueline incluso decidió hacerse monja, mientras que
Pascal, que sufría fenómenos de parálisis en las piernas con permanentes
dolores, interpretó su enfermedad como signo divino y empezó a llevar una vida
ascética.
Sin embargo, el propio Pascal nunca consideró que su devoción
fuera un obstáculo para seguir dedicándose a sus estudios en ciencias naturales
y matemáticas. Así, por ejemplo, ya en 1646 repitió con éxito los ensayos que Evangelista Torricelli había realizado en 1643 para demostrar
la existencia del vacío, la que
hasta entonces se había considerado como imposible, publicando en 1647 sus
resultados en el Tratado sobre el vacío.
A partir de mayo de 1647 volvió a vivir con Jacqueline y poco
después también con su padre, principalmente en París, donde contactó a los
principales jansenistas, pero
también continuó con sus investigaciones. Sus ideas no fueron bien recibidas
por numerosos teólogos e investigadores, entre ellos Descartes con el que se reunió repetidas veces
en París a fines de septiembre de 1647. Por ello a partir de entonces formuló
sus especulaciones sobre el vacío y el éter de una forma más indirecta,
particularmente en un tratado sobre la presión
atmosférica, demostrando su dependencia de la altura del lugar en cuestión, por
medio de experimentos que hizo realizar a su cuñado Périer
en el Puy de Dome en 1648. También en 1648, en otro
tratado, fundamentó la ley de los vasos
comunicantes.
Pocos años antes (en 1644), Torricelli había publicado su experimento por el
que el peso del aire de la atmósfera mantenía el mercurio en un tubo, con vacío
en su parte superior, demostrando que el aire ejerce una presión debido a su
peso. Pascal no estaba convencido de esa teoría, y seguía siendo partidario de
la teoría del Horror vacui. Para
confirmarlo, pidió a su cuñado que escalase el volcán Puy de Dôme hasta su cima, y se comprobó que el
mercurio sube más en la base de la montaña que en su cima. Tras el experimento,
Pascal abandonó la teoría del Horror vacui y se convirtió a la teoría de la
causa mecanicista.
En otoño de 1651 murió Pascal padre. Poco después y contraviniendo
los deseos tanto del fallecido como también de Blaise, Jacqueline se incorporó
al convento estrictamente jansenista de Port
Royal en París.
Ahora, Pascal por primera vez dependía nada más que de sí mismo.
Ya que, si bien no era rico, sí tenía una situación acomodada y era noble,
comenzó a frecuentar la sociedad de París, trabando amistad con el joven duque
de Roannez, con el que compartía el interés por la
filosofía. Éste lo llevó de viaje en 1652, junto a algunos de sus amigos
librepensadores, entre ellos Chevalier de Méré, oportunidad en
la que Pascal se introdujo en la filosofía moderna, aprendiendo además el arte
de las conversaciones sociales. Gracias a que frecuentaba el salón esteta de Madame de Sablé,
se compenetró también con las «bellas letras» de su época. Incluso llegó brevemente a pensar en
comprar un cargo y en casarse. Sin embargo, una obra que se le adjudicó por
mucho tiempo, al amoldarse en cierto sentido a esta fase mundana de su vida, el
anónimo Discurso acerca de las
Pasiones del Amor, que no es de su autoría.
En 1653 escribió un tratado sobre la presión atmosférica, en el
que por primera vez en la historia de la ciencia se hace una descripción
completa de la hidrostática.
Junto a sus nuevos conocidos, especialmente con el Chevalier de Méré, Pascal también
tenía discusiones acerca del modo de ganar en los juegos de azar, un pasatiempo
típicamente de nobles. Esto lo llevó en 1653 a dedicarse a la teoría de la probabilidad,
estudiándola en 1654 en su intercambio epistolar con el juez de Toulouse y destacado matemático Pierre de Fermat. Analizaron
principalmente los juegos de dados. Al mismo tiempo, Pascal se ocupó de otros
problemas matemáticos, publicando diversas obras en 1654: Teoría de probabilidad y combinatoria, el Traité
du triangle arithmétique acerca del llamado triángulo de Pascal y los coeficientes binomiales, en el que
también por primera vez formuló explícitamente el principio de demostración por inducción matemática, el Traité des ordres numériques acerca
de los órdenes de los números y Combinaisons sobre
combinaciones de números.
En otoño de 1654, Pascal sufrió un trastorno depresivo. Volvió a
acercarse a Jacqueline, visitándola con frecuencia en el convento y se mudó a
otro barrio para alejarse de sus amigos mundanos. Sin embargo, siguió
trabajando en cuestiones matemáticas y otros asuntos científicos. Después se
retiró por completo de la sociedad parisina para dedicarse por completo a su
devoción.
Aparte de su trabajo en los Pensées, volvió a emprender también estudios
matemáticos. Así, en 1658, calculó la superficie de la cicloide con los métodos de Cavalieri,
así como el volumen del sólido de rotación que
resulta de una rotación de la ciclode alrededor del eje de las x.
En 1659 apareció su escrito Tratado
de los senos de los cuadrantes circulares. Cuando Gottfried Leibniz leyó esta obra en 1673 en París,
recibió de ella un impulso decisivo para desarrollar el cálculo infinitesimal considerando el razonamiento
específico por parte de Pascal, que Leibniz empleó de manera más general,
interpretando el círculo de Pascal como círculo de curvatura en determinados
puntos de una función o curva cualquiera. Leibniz dice que en ello había visto
una luz que el propio autor no vio. De allí se origina el concepto de triángulo característico.
Su salud deteriorada empeoró cada vez más deprisa en esos años,
probablemente a consecuencia de su modo de vida extremadamente ascético, que lo
debilitaba más.
A principios de 1662, junto a su amigo Roannez,
fundó una empresa de carrozas “Las carrozas de cincuenta centavos”, marcando el
comienzo del transporte público local en París.
En agosto enfermó gravemente, hizo vender sus enseres domésticos donándolos
para fines de caridad y murió, a la edad de solo 39 años, un año después de la
muerte de su hermana Jacqueline, en casa de los Périer
en París.
JOHN WALLIS

John Wallis (1616 – 1703), fue un matemático inglés a quien se atribuye en parte el desarrollo del cálculo moderno. Fue un precursor del cálculo infinitesimal (introdujo la utilización del símbolo ∞ para
representar la noción de infinito). Entre 1643 y 1689 fue criptógrafo del Parlamento y posteriormente de la Corte real. Fue también uno de los
fundadores de la Royal Society y
profesor en la Universidad
de Oxford.
Nació en Ashford, Inglaterra, fue el
tercero de los cinco hijos del reverendo John Wallis y Joanna Chapman. Inició
su educación en la escuela local de Ashford, pero se
trasladó a la escuela James Movat en Tenterden en 1625 debido al brote de una plaga.
Con la intención de que obtuviera un doctorado, en 1632 fue
enviado al Emmanuel College en Cambridge. Allí, defendió un argumento
sobre la doctrina de la circulación de la sangre; se considera que fue la
primera vez en Europa que esta teoría era públicamente mantenida en una
discusión. En cualquier caso, sus intereses seguían centrados en las
matemáticas. Obtuvo la licenciatura en
Artes en 1637 y un Máster en 1640,
posteriormente se incorporó al sacerdocio. Se le concedió una beca para
estudiar en Cambridge en 1644, lo cual no le impidió continuar con sus planes
de su boda con Susana Glyde celebrada el 14 de marzo de 1645.
De regreso a Londres (en 1643 había sido nombrado capellán de San
Gabriel en Fenchurch Street), Wallis se une al grupo
de científicos que posteriormente formarían la Royal Society.
En poco tiempo, empezó a escribir sus propios tratados sobre un amplio número
de materias, a lo largo de su vida, Wallis realizó contribuciones
significativas a la trigonometría,
el cálculo, la geometría y el análisis de las series infinitas.
John Wallis se unió a los Presbiterianos moderados apoyando la proposición
contra la ejecución de Carlos I,
lo cual le valió la permanente hostilidad de los Independentistas. A pesar de
su oposición, fue propuesto en 1649 para ocupar la Cátedra Savilian de Geometría en la Universidad de Oxford, dónde vivió
hasta su muerte el 28 de octubre de 1703.
Al margen de sus trabajos en matemáticas, también escribió sobre teología, lógica, gramática inglesa y filosofía; asimismo, fue uno de los
pioneros en la introducción en Inglaterra de un sistema de enseñanza para sordomudos,
inspirado en el método del español Juan
de Pablo Bonet.
En 1655, Wallis
publicó un tratado sobre secciones cónicas en el que las define analíticamente.
Este fue el primer libro en el que estas curvas fueron consideradas y definidas
como curvas de segundo grado. Contribuyó a eliminar algunas de las dificultades
y oscuridades presentes en los trabajos de René
Descartes sobre geometría
analítica.
En 1656 se publicó Arithmetica
Infinitorum, el trabajo más importante de Wallis.
En este tratado, los métodos de análisis de Descartes y Cavalieri fueron ampliados y sistematizados,
aunque algunas ideas recibieron críticas. Tras un corto periodo centrado en las
secciones cónicas, comenzó desarrollando una notación estándar para las
potencias, ampliándola desde los números
enteros positivos hasta los números
racionales.
Pocos años después, en 1659,
Wallis publica un tratado con la solución a los problemas de las cicloides propuestos por Blaise Pascal. En él, explica cómo los
principios aportados en su Arithmetica Infinitorum pueden
utilizarse para el cálculo de la longitud de curvas algebraicas y da una solución al
problema del cálculo de la longitud de la parábola semicúbica x³ = ay², descubierta en 1657
por su pupilo William Neil.
Puesto que todos los intentos para el cálculo de la longitud de la elipse y la
hipérbola habían sido ineficaces, se había supuesto que la longitud de ninguna
curva podría ser calculada (con excepción de la circunferencia) como de hecho
Descartes había afirmado que era el caso. La espiral
logarítmica fue la primera línea curva cuya
longitud fue calculada, cálculo hecho por Evangelista Torricelli, pero la
ampliación de Neil y Wallis a cualquier curva algebraica fue una novedad.
Antes, en 1658, un descubrimiento similar, pero independiente del
de Neil, fue realizado por van Heuraët, y publicado en 1659 por van Schooten en su edición de la Descartes's
Geometría. La solución aportada por Neil y Wallis era muy similiar aunque no enunciaba ninguna regla general y el
razonamiento era algo torpe. Un tercer método fue sugerido por Fermat en 1660,
pero era laborioso y poco elegante.
Se considera a Wallis el autor de la idea de
la recta de números enteros, en la cual los números se representan
geométricamente en una línea con los positivos aumentando hacia la derecha y
los negativos hacia la izquierda. De igual forma fue Wallis quien representó
por primera vez gráficamente a los números imaginarios.

Gilles Personne de Roberval (1602
- 1675), fue un matemático francés. Su nombre era originalmente Gilles Personne,
antes que del de Roberval, por el que se le conoce,
dado el lugar de su nacimiento.
Roberval fue uno de los
matemáticos que, justo antes de la invención del cálculo infinitesimal, ocuparon su
atención en problemas que implican límites o infinitesimales, que hoy en día se
pueden resolver por cálculo. Trabajó en el cálculo del área de superficies y la
cubicación de los sólidos, él logró hacer estos cálculos por un método original
que él llamó el "método de los indivisibles", pero mantuvo su método
para su propio uso y no lo publicó, en tanto que Bonaventura
Cavalieri publicó un método similar que él inventó de
forma independiente.
Otro de los descubrimientos de Roberval
fue un método muy general para dibujar tangentes,
considerando una curva descrita por un punto móvil cuyo
movimiento es el resultado de varios movimientos simples.
Entre Roberval y René Descartes existía cierto
resentimiento, debido a las críticas de Descartes a algunos de los métodos
empleados por Roberval y por Pierre de Fermat, esto lo llevó a
criticar y a oponerse a los métodos
analíticos que Descartes introdujo en la geometría en este tiempo.

René Descartes (1596-1650), filósofo, científico y
matemático francés, considerado el fundador de la filosofía moderna.
Nació en La Haye, hoy Descartes
(Indre-et-Loire), era hijo de un miembro de la baja nobleza y pertenecía a una
familia que había dado algunos hombres doctos. Cuando tenía ocho años de edad
fue enviado al colegio jesuítico de La Flèche (en Anjou), donde permaneció 10 años. Junto a las disciplinas
clásicas tradicionales, también aprendió matemáticas y las principales
doctrinas del escolasticismo, tendentes a orientar la razón humana hacia la
comprensión de la doctrina cristiana. El catolicismo ejerció una gran
influencia en Descartes a lo largo de toda su vida. Tras concluir su periodo de
formación primaria en dicho centro, cursó estudios de Derecho en la Universidad
de Poitiers, donde se licenció en 1616. Sin embargo, nunca llegó a ejercer como
jurista. En 1618 entró al servicio del príncipe Mauricio I de Nassau-Orange,
con la intención de seguir la carrera militar; posteriormente sirvió en otros
ejércitos. Pero su interés se centró siempre en los problemas de las
matemáticas y la filosofía, a los que dedicó el resto de su vida. Tras realizar
numerosos viajes residió en París de 1625 a 1628. Durante este periodo se
dedicó al estudio de la filosofía y también realizó experimentos de óptica. En
1628, después de vender las propiedades que poseía en Francia, se trasladó a
las Provincias Unidas y vivió en diferentes ciudades (Amsterdam,
Deventer, Utrecht y Leiden).
Su contribución más notable a las matemáticas fue la
sistematización de la geometría analítica. Fue el primer matemático que intentó
clasificar las curvas conforme al tipo de ecuaciones que las producen y
contribuyó también a la elaboración de la teoría de las ecuaciones. Fue el
responsable de la utilización de las últimas letras del alfabeto para designar
las cantidades desconocidas y las primeras letras para las conocidas. También
inventó la notación de los exponentes (como x2) para indicar las
potencias de los números. Además, formuló la regla de los signos para descifrar
el número de raíces negativas y positivas de cualquier ecuación algebraica.
JOHANNES KEPLER

Johannes Kepler (1561 - 1630), nació en el seno de una familia de religión protestante luterana, instalada en la ciudad de Weil der Stadt en Baden-Wurtemberg,
Alemania. Su abuelo había sido el alcalde de la ciudad, pero cuando nació
Kepler, la familia se encontraba en decadencia. Su padre, Heinrich Kepler, era
mercenario en el ejército del Duque de Wurtemberg y,
siempre en campaña, raramente estaba presente en su domicilio. Su madre, Katherina Guldenmann, que llevaba una casa de huéspedes, era
curandera y herborista, más tarde fue acusada de brujería. Kepler, nacido
prematuramente a los siete meses de embarazo e hipocondríaco de naturaleza endeble, sufrió toda su
vida una salud frágil. A la edad de tres años,
contrae la viruela, lo que, entre
otras secuelas, debilitará su vista severamente. A pesar de su salud, fue un
niño brillante que gustaba impresionar a los viajeros en la hospedería de su madre
con sus fenomenales facultades matemáticas. De 1574 a 1576, vivió con Heinrich (que era epiléptico) en casa de sus abuelos
mientras que su padre estaba en una campaña y su madre había ido en su busca.
Al regresar sus padres, Kepler se trasladó a Leonberg y entra en la escuela latina en 1577. Sus padres le despertaron el
interés por la astronomía. Con
cinco años, observó el cometa de 1577, comentando que su madre lo
llevó a un lugar alto para verlo. Su padre le mostró a la edad de nueve años el eclipse de luna del 31
de enero de 1580, recordando que la Luna aparecía
bastante roja. Kepler estudió más tarde el fenómeno y lo explicó en una de sus
obras de óptica. Su padre partió
de nuevo para la guerra en 1589,
desapareciendo para siempre.
En 1584, Kepler
entró en el Seminario protestante de Adelberg y dos
años más tarde, en el Seminario superior de Maulbronn. Obtuvo allí su diploma de fin de estudios y se
matriculó en 1589 en la universidad de Tubinga. Comenzó
primero por estudiar ética, dialéctica, retórica, griego, hebreo, astronomía y
física, y más tarde teología y ciencias humanas. Continuó con sus estudios
después de obtener la maestría en 1591.
Su profesor de matemáticas, el astrónomo Michael
Maestlin, le enseñó el sistema heliocéntrico de Copérnico que se reservaba a los mejores
estudiantes. Los otros estudiantes tomaban como cierto el sistema geocéntrico de Ptolomeo,
que afirmaba que la Tierra estaba inmóvil y ocupaba el centro del Universo y que el Sol, la Luna, los planetas y las estrellas giraban a su alrededor. Kepler se hizo
así un copernicano convencido y mantuvo una relación muy estrecha con Maestlin; no vaciló en pedirle ayuda o consejo para sus
trabajos.
Mientras Kepler planeaba hacerse ministro luterano, la escuela
protestante de Graz buscaba a un profesor de matemáticas.
Abandonó entonces sus estudios de Teología para tomar el puesto y dejó Tubinga
en 1594. En Graz, publicó
almanaques con predicciones astrológicas –que él escribía– aunque negaba
algunos de sus preceptos. En la época, la distinción entre ciencia y creencia
no estaba establecida todavía claramente y el movimiento de los astros, todavía
bastante desconocido, se consideraba gobernado por leyes divinas.
Kepler estuvo casado dos veces, la primera de ellas con Bárbara
Müller con quien tuvo cinco hijos y con Susanne Reuttinger con la que tuvo siete niños.
En 1615,
su madre, entonces a la edad de 68 años, fue acusada de brujería. Kepler,
persuadido de su inocencia, pasó seis años trabajando en su defensa ante los
tribunales y escribiendo numerosos alegatos. Debió regresar dos veces a Wurtemberg. Ella pasó un año encerrada en la torre de Güglingen, a expensas de Kepler, habiendo escapado por poco
de la tortura. Finalmente, fue liberada el 28 de septiembre de 1621.
Debilitada por los duros años de proceso y de encarcelamiento, murió seis meses
más tarde. En 1628 Kepler pasó al servicio de Albrecht von Wallenstein, en Silesia,
quien le prometió, en vano, resarcirle de la deuda contraída con él por la
Corona a lo largo de los años. Un mes antes de morir, víctima de la fiebre,
Kepler abandonó Silesia en busca de un nuevo empleo. Kepler murió en 1630 en
Ratisbona, en Baviera, Alemania, a la edad de 58 años.
En 1632, durante la Guerra de los Treinta Años, el ejército sueco destruyó su tumba y se perdieron sus trabajos hasta el año
1773. Recuperados por Catalina
II de Rusia, se encuentran actualmente en el Observatorio de Pulkovo en San Petersburgo, Rusia.
El método de integración geométrica que se
consideraba ideal durante la primera mitad del siglo XVII era el método de exhaución que había sido inventado por Eudoxo
y perfeccionado por Arquímedes. El nombre es desafortunado porque la idea
central del método es la de evitar el infinito y por lo tanto, este método no
lleva a un “agotamiento” de la figura a determinar.
Entre los matemáticos del siglo XVII era general el
deseo de encontrar un método para obtener resultados en problemas de
cuadraturas y que, a diferencia del método de exhaución,
fuera directo. Y sería mejor si el nuevo método, aparte de dar resultados,
pudiera ser utilizado para demostrarlos.
El camino que siguieron fue el que se deriva de una
concepción intuitiva inmediata de las magnitudes geométricas. Se imaginaron un
área como formada, por ejemplo, por un número infinito de líneas paralelas.
Kepler ya había hecho uso de métodos infinitesimales en sus obras; el interés
que se tomó en el cálculo de volúmenes de toneles de vino dio como resultado un
libro Nova stereometria
doliurum vinariorum
(1615). En él consideraba sólidos de revolución como si estuvieran compuestos
de diversas maneras por una cantidad infinita de partes sólidas. Por ejemplo,
consideraba una esfera como formada por un número infinito de conos con vértice
común en el centro y base en la superficie de la esfera. Esto le conducía al
resultado de que la esfera es igual en volumen al cono que tiene como altura el
radio de la esfera y como base un círculo igual al área de la esfera, es decir,
un círculo con el diámetro de la esfera como radio.

Pierre de Fermat (1601-1665),
matemático francés. Poco se conoce de sus primeros años, excepto que estudió
derecho, posiblemente en Toulouse y Burdeos. Pasó
toda su vida en el sur de Francia, lejos de los grandes centros europeos del
saber. No era matemático profesional, sino jurista y ninguno de sus trabajos de
matemáticas vio la luz pública hasta después de su muerte. Interesado por las matemáticas, en 1629 abordó la tarea de reconstruir
algunas de las demostraciones perdidas del matemático griego Apolonio relativas
a los lugares geométricos. Desarrolló contemporánea e independientemente de
René Descartes, un método algebraico para tratar cuestiones de geometría por
medio de un sistema de coordenadas.
Diseñó también un algoritmo de
diferenciación mediante el cual pudo determinar los valores máximos y mínimos
de una curva polinómica, trabajo que abrió el camino al desarrollo posterior
del cálculo infinitesimal de Leibniz. Tras asumir correctamente que cuando la luz
se desplaza en un medio más denso su velocidad disminuye, demostró que el
camino de un rayo luminoso entre dos puntos es siempre aquel que menos tiempo
le cuesta recorrer; de dicho principio, que lleva su nombre, se deducen las
leyes de la reflexión y la refracción. En 1654 desarrolló con Blaise Pascal los principios de la teoría de la probabilidad.
Otro campo en el que realizó destacadas
aportaciones fue el de la teoría de números, en la que empezó a interesarse
tras consultar una edición de la Aritmética de Diofanto;
precisamente en el margen de una página de dicha edición fue donde anotó el
célebre teorema que lleva su nombre y que tardaría más de tres siglos en
demostrarse: “Es imposible encontrar la forma de convertir un cubo en la suma
de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en
general cualquier potencia más alta que el cuadrado, en la suma de dos
potencias de la misma clase”. He descubierto para el hecho una demostración
excelente. Pero este margen es demasiado pequeño para que (la demostración)
quepa en él. De su trabajo en dicho campo se derivaron importantes resultados
relacionados con las propiedades de los números primos, muchas de las cuales
quedaron expresadas en forma de simples proposiciones y teoremas.
Desarrolló también un ingenioso método
de demostración que denominó «del descenso infinito». Extremadamente prolífico,
sus deberes profesionales y su particular forma de trabajar (sólo publicó una
obra científica en vida) redujeron en gran medida el impacto de su obra.

Galileo
Galilei (1564-1642), físico y astrónomo italiano que, junto con
el astrónomo alemán Johannes Kepler, comenzó la revolución científica que
culminó con la obra del físico inglés Isaac Newton. Su principal contribución a
la astronomía fue el uso del telescopio para la observación y descubrimiento de
las manchas solares, valles y montañas lunares, los cuatro satélites mayores de
Júpiter y las fases de Venus. En el campo de la física descubrió las leyes que
rigen la caída de los cuerpos y el movimiento de los proyectiles. En la
historia de la cultura, Galileo se ha convertido en el símbolo de la lucha
contra la autoridad y de la libertad en la investigación.
Nació cerca de Pisa el 15 de
febrero de 1564. Su padre, Vincenzo Galilei, ocupó un
lugar destacado en la revolución musical que supuso el paso de la polifonía
medieval a la modulación armónica. Del mismo modo que Vincenzo
consideraba que las teorías rígidas impedían la evolución hacia nuevas formas
musicales, su hijo mayor veía la teología física de Aristóteles como un freno a
la investigación científica. Galileo estudió con los monjes en Vallombroso y en 1581 ingresó en la Universidad de Pisa
para estudiar medicina. Al poco tiempo cambió sus estudios de medicina por la
filosofía y las matemáticas, abandonando la universidad en 1585 sin haber
llegado a obtener el título. Durante un tiempo dio clases particulares y
escribió sobre hidrostática y el movimiento natural, pero no llegó a publicar
nada. En 1589 trabajó como profesor de matemáticas en Pisa, donde se dice que
demostró ante sus alumnos el error de Aristóteles, que afirmaba que la
velocidad de caída de los cuerpos era proporcional a su peso, dejando caer
desde la torre inclinada de esta ciudad dos objetos de pesos diferentes. En
1592 no le renovaron su contrato, posiblemente por oponerse a la filosofía
aristotélica. Ese mismo año fue admitido en la cátedra de matemáticas de la
Universidad de Padua, donde permaneció hasta 1610.
En Padua, Galileo inventó un “compás”
de cálculo que resolvía problemas prácticos de matemáticas. De la física
especulativa pasó a dedicarse a las mediciones precisas, descubrió las leyes de
la caída de los cuerpos y de la trayectoria parabólica de los proyectiles,
estudió el movimiento del péndulo e investigó la mecánica y la resistencia de
los materiales. Apenas mostraba interés por la astronomía, aunque a partir de
1595 se inclinó por la teoría de Copérnico, que sostenía que la Tierra giraba
alrededor del Sol desechando el modelo de Aristóteles y Tolomeo en el que los
planetas giraban alrededor de una Tierra estacionaria. Solamente la concepción
de Copérnico apoyaba la teoría de las mareas de Galileo, que se basaba en el
movimiento de la Tierra. En 1609 oyó decir que en los Países Bajos habían
inventado un telescopio. En agosto de ese año presentó al duque de Venecia un
telescopio de una potencia similar a los modernos gemelos o binoculares. Su
contribución en las operaciones navales y marítimas le supuso duplicar sus
ingresos y la concesión del cargo vitalicio de profesor.
En diciembre de 1609 Galileo
había construido un telescopio de veinte aumentos, con el que descubrió
montañas y cráteres en la Luna. También observó que la Vía Láctea estaba
compuesta por estrellas y descubrió los cuatro satélites mayores de Júpiter. En
marzo de 1610 publicó estos descubrimientos en El mensajero de los astros.
Su fama le valió el ser nombrado matemático de la corte de Florencia, donde
quedó libre de sus responsabilidades académicas y pudo dedicarse a investigar y
escribir. En diciembre de 1610 pudo observar las fases de Venus, que
contradecían la astronomía de Tolomeo y confirmaban su aceptación de las
teorías de Copérnico.
Los profesores de filosofía se
burlaron de los descubrimientos de Galileo, dado que Aristóteles había afirmado
que en el cielo sólo podía haber cuerpos perfectamente esféricos y que no era
posible que apareciera nada nuevo. También discrepaba Galileo de los profesores
de Florencia y Pisa sobre la hidrostática, y en 1612 publicó un libro sobre
cuerpos en flotación. Como respuesta, aparecieron inmediatamente cuatro
publicaciones que atacaban a Galileo y rechazaban su física. En 1613 escribió
un tratado sobre las manchas solares y anticipó la supremacía de la teoría de
Copérnico. En su ausencia, un profesor de Pisa le dijo a la familia de los
Medici (que gobernaban Florencia y mantenían a Galileo) que la creencia de que
la Tierra se movía constituía una herejía. En 1614, un sacerdote florentino
denunció desde el púlpito a Galileo y a sus seguidores. Éste escribió entonces
una extensa carta abierta sobre la irrelevancia de los pasajes bíblicos en los
razonamientos científicos, sosteniendo que la interpretación de la Biblia
debería ir adaptándose a los nuevos conocimientos y que ninguna posición
científica debería convertirse en artículo de fe de la Iglesia católica.
A principios de 1616, los libros de
Copérnico fueron censurados por un edicto, y el cardenal jesuita Roberto
Belarmino dio instrucciones a Galileo para que no defendiera la teoría de que
la Tierra se movía. El cardenal Belarmino le había avisado previamente de que
sólo tuviera en cuenta sus ideas como hipótesis de trabajo e investigación, sin
tomar literalmente los conceptos de Copérnico como verdades y sin tratar de
aproximarlos a lo escrito en la Biblia. Galileo guardó silencio sobre el tema
durante algunos años y se dedicó a investigar un método para determinar la
latitud y longitud en el mar basándose en sus predicciones sobre las posiciones
de los satélites de Júpiter, así como a resumir sus primeros trabajos sobre la
caída de los cuerpos y a exponer sus puntos de vista sobre el razonamiento
científico en una obra sobre los cometas, El ensayador (1623).
En 1624 Galileo empezó a escribir un
libro que quiso titular Diálogo sobre las mareas, en el que abordaba las
hipótesis de Tolomeo y Copérnico respecto a este fenómeno. En 1630 el libro
obtuvo la licencia de los censores de la Iglesia católica de Roma, pero le
cambiaron el título por Diálogo sobre los sistemas máximos, publicado en
Florencia en 1632. A pesar de haber obtenido dos licencias oficiales, Galileo
fue llamado a Roma por la Inquisición a fin de procesarle bajo la acusación de
“sospecha grave de herejía”. Este cargo se basaba en un informe según el cual
se le había prohibido en 1616 hablar o escribir sobre el sistema de Copérnico.
El cardenal Belarmino había muerto, pero Galileo facilitó un certificado con la
firma del cardenal, según el cual no sufriría en el futuro ninguna otra
restricción que no fueran las que para todo católico romano contenía un edicto
de 1616. Este escrito no pudo ser rebatido por ningún documento, pero Galileo
fue obligado a abjurar en 1633 y se le condenó a prisión perpetua (condena que
le fue conmutada por arresto domiciliario). Los ejemplares del Diálogo
fueron quemados y la sentencia fue leída públicamente en todas las
universidades.
Con respecto al ejercicio de las matemáticas que hace
Galileo, podemos señalar dos aspectos: el primero está relacionado con las
matemáticas griegas o “clásicas”, donde usa intensivamente la teoría euclidiana
de las proporciones, las cónicas de Apolonio (sobre todo en la descripción del
movimiento parabólico) y los desarrollos matemáticos de Arquímedes. El
extraordinario uso que hace Galileo de las matemáticas clásicas se encuentra
expuesto en su obra fundacional “Discursos y demostraciones matemáticas en
torno a dos nuevas ciencias”.
El segundo, tiene que ver con “aportaciones” galileanas
tales como los diagramas tiempo-velocidad, una herramienta invaluable para el
estudio de la cinemática; la composición de movimientos, que llevaría a la
noción de vector; el atomismo matemático y su intuición acerca de algunas
nociones, hoy bien fundamentadas, del cálculo infinitesimal; entre las que tenemos
el agregatum o massa,
relacionado con lo que hoy se conoce como integración y concebido para el
estudio del movimiento uniformemente acelerado, en donde Galilei se apoyó, a la
manera de Nicolás de Oresme, en los gráficos.
Finalmente, no se puede dejar de mencionar el abordaje que
hace Galileo del asunto relativo al concepto de infinito en relación con las
magnitudes extensas (quante) o numerables; e
inextensas (non quante), no divisibles, a las que
considera como las primeras componentes de las magnitudes. Su discípulo Cavalieri se encargaría de llevar más lejos algunas de
éstas nociones.
La última obra de Galileo, Consideraciones
y demostraciones matemáticas sobre dos ciencias nuevas relacionadas con la
mecánica, publicada en Leiden en 1638, revisa y afina sus primeros estudios
sobre el movimiento y los principios de la mecánica en general. Este libro
abrió el camino que llevó a Newton a formular la ley de la gravitación
universal, que armonizó las leyes de Kepler sobre los planetas con las
matemáticas y la física de Galileo.
La contribución más importante de
Galileo a la ciencia fue su descubrimiento de la física de las mediciones
precisas, más que los principios metafísicos y la lógica formal. Sin embargo,
tuvieron más influencia sus libros El mensajero de los astros y el Diálogo,
que abrieron nuevos campos en la astronomía. Más allá de su labor científica,
Galileo destaca como defensor de una investigación libre de interferencias
filosóficas y teológicas. Desde la publicación de la documentación completa del
juicio contra Galileo en 1870, toda la responsabilidad de la condena a Galileo
ha recaído tradicionalmente sobre la Iglesia católica de Roma, encubriendo la
responsabilidad de los profesores de filosofía que persuadieron a los teólogos
de que los descubrimientos de Galileo eran heréticos. Juan Pablo II abrió en
1979 una investigación sobre la condena eclesiástica del astrónomo para su
posible revisión. En octubre de 1992, una comisión papal reconoció el error del
Vaticano.
BONAVENTURA
FRANCESCO CAVALIERI

Bonaventura Cavalieri (1598 - 1647), matemático italiano perteneciente a la orden de los jesuitas. Fue alumno de Galileo Galilei, y enseñó matemáticas
en Bolonia (1629). Su interés por las matemáticas fue estimulado por los
trabajos de Euclides y luego de encontrar a Galileo, se
consideró como un discípulo de este astrónomo. En Pisa, Cavalieri
fue educado en matemáticas por Benedetto
Castelli, un profesor de matemáticas en la Universidad de esa ciudad. En 1629 Cavalieri fue nombrado profesor de matemáticas en Bolonia.
Fue el primero en introducir en Italia el cálculo logarítmico, pero debe su
celebridad a su teoría de los «indivisibles», que expuso en Geometria
indivisibilibus continuorum
quadam nova ratione promota (1635).
Esta teoría estudia las magnitudes geométricas como compuestas de un número infinito de elementos, o indivisibles,
que son los últimos términos de la descomposición que se puede hacer. La medida
de las longitudes, de las superficies y de los volúmenes se convierte en
efectuar la suma de la infinidad de indivisibles: es el principio del cálculo
de una integral definida, aunque sin la noción rigurosa moderna de paso al límite. Por esto puede ser
considerado como uno de los precursores del análisis infinitesimal moderno. El Principio de Cavalieri se fundamenta en esta teoría.
Asimismo figuró entre los primeros que enseñaron la teoría
copernicana de los planetas. Otros trabajos suyos dignos de renombre son el
desarrollo dado a la trigonometría
esférica, así como el descubrimiento de las fórmulas relativas a los focos de
los espejos y de las lentes.

Evangelista Torricelli (1608
- 1647), fue un físico y matemático italiano. Sus padres
fueron Gaspare Torricelli y Caterina Angetti. Era una familia humilde, Gaspare
era obrero textil. Evangelista Torricelli fue
el mayor de los tres hijos del matrimonio.
Sus padres notaron el talento de su hijo y como no
tenían recursos para educarlo lo enviaron a estudiar con su tío, el Hermano Jacopo, un monje Camaldolese, al
colegio Jesuita entre los años 1624-1626 en Faenza.
Su tío observa el talento de Evangelista
Torricelli y
arregla que estudie privadamente con otro monje Camatdolese,
Benedetto Castetli, de quien se convierte en ayudante
hasta 1632. Castelli enseñaba en la Universidad de Sapienza,
en Roma. Torricelli reemplazaba
a Castelti cuando estaba ausente de Roma.
El 11 de septiembre de 1632 Castelli escribió
a Galileo una
carta en la cual informa sobre los notables progresos científicos de Evangelista Torricelli. Galileo
le contesta a Castelli, pero como éste no estaba en Roma, su secretario Torricelli aprovecha para
contestar la carta y explicarle directamente a Galileo sobre sus trabajos
matemáticos. Durante los siguientes nueve años (1632-1641), fue secretario de
Giovanni Ciampoli, amigo de Galileo y de otros
profesores.
No se sabe exactamente donde vivió Torricelli durante estos
años, pero como Ciampoli fue gobernador de muchas
ciudades, debe haber vivido en distintos períodos en Montatto,
Norcia, San Severino y Fabriano.
Para 1641 Torricelli había
completado gran parte del trabajo que iba a publicar en tres partes en
1644, Opera geométrica. La segunda parte del trabajo es
el De motu gravium, que es un
tratado sobre el movimiento parabólico de los proyectiles. Torricelli pidió opinión
a Castelti sobre el tratado en 1641.
Castelti estaba tan
impresionado que él mismo le escribió a Galileo, que vivía en Arcetri, cerca de Florencia, vigilado por la Inquisición. En abril de
1641 Castelli fue a Venecia y de paso se detuvo en Arcetri
para entregarte a Galileo una copia del manuscrito de Torricelli y le sugiere que lo
contrate como asistente.
Mientras Castelli viajaba, Torricelli permanecía en Roma a
cargo de sus clases. Galileo aceptó la propuesta de Castelli y el 10 de octubre
de 1641, Torricelli llegó
a la casa de Galileo en Arcetri.
Se convirtió así en su discípulo en 1641.
Permaneció viviendo con Galileo durante
su ceguera, cuidándolo hasta el día de su muerte en enero de 1642 y, un año más
tarde, lo sucedió en el cargo de matemático de la corte del Gran Duque Fernando
II de Toscana, pero no recibió el título de Filósofo de la Corte, que tenía
Galileo. Torricelli mantuvo
este cargo hasta su muerte, viviendo en el palacio ducal en Florencia.
Otro discípulo de Castelli era Cavalieri, que
era titular de la cátedra de Matemática en Bolonia. Torricelli estudió los
métodos de Cavalieri y al principio desconfió de
ellos. Pero pronto se convenció de su exactitud y comenzó a
profundizarlos.
Uno de sus resultados más importante tiene que ver con la extensión del método
de los indivisibles de Cavalieri a los indivisibles curvo. Para 1641 había probado un
número impresionante de resultados usando el método que publicaría tres años
después. Examinó los cuerpos tridimensionales que se obtienen al rotar un
polígono regular alrededor de un eje de simetría. También calculó el área y el centro
de gravedad de la cicloide.
El tema de La cicloide surgió de una disputa
con Roberval. En una carta fechada en
octubre de 1643 le informa a Roberval sobre
sus puntos de vista y resultados sobre el centro de gravedad de la parábola, la superficie de la cicloide y su
historia, el sólido de revolución generado por una cónica y un sólido
hiperbólico. No hay duda que ambos matemáticos llegaron a
descubrimientos similares sobre La cicloide pero que ninguno influyó sobre la
ideas del otro. Otra contribución de Torricelli fue en 1640, la resolución del problema de Fermat:
dados tres puntos en un plano,
encontrar un Cuarto punto tal que la suma de las distancias a los tres dados
sea la menor posible (conocido como el centro isogónico del triángulo). Torricelli fue
la primera persona en crear un vacío sustentable, su nombre se asocia a la
invención del barómetro de mercurio en 1644 para la medición de la presión
atmosférica.
Este experimento, además de la importancia de sus
aplicaciones prácticas, permitía demostrar la inconsistencia de las
afirmaciones de los que aún seguían las teorías aristotélicas sobre la
imposibilidad de la existencia de vacío, ya que por encima de la columna de
mercurio de su barómetro se producía dicho vacío.
En De
motu gravium también probó que la velocidad de salida de un líquido a
través de un pequeño orificio en la pared delgada de un recipiente es
proporcional a la raíz cuadrada de la altura entre el orificio y la base del
recipiente, enunciado conocido como el Teorema de Torricelli. Algunos lo consideran el
fundador de la hidrodinámica.
En esta publicación estudia el movimiento de un
proyectil, desarrolla las ideas de Galileo sobre la trayectoria parabólica de
un proyectil lanzado horizontalmente y da una teoría sobre los proyectiles
disparados en cualquier ángulo. Por otra parte, construyó los mejores anteojos
de la época y hasta ahora, las lentes preparadas por él, se destacan por su
perfección. También construyó telescopios y microscopios. Aparentemente
aprendió estas técnicas mientras vivió con Galileo. Torricelli ganó mucho dinero por
sus habilidades en la construcción de lentes durante la última parte de su vida
en Florencia y recibió muchos regalos del GranDuque. En
1647 Torricelli; contrajo
fiebre tifoidea y murió a los 39 años.
Hasta el siglo XVII era imposible aceptar la idea
de que el vacío era parte del espacio. Aristóteles había intentado sin éxito
verificar el peso del aire y durante mucho tiempo el pensamiento imperante
afirmaba que el vacío era, sobre todo, un concepto inconsistente. Sin embargo,
el camino de la investigación y la experimentación, iniciado en gran medida por
los descubrimientos de Galileo, Newton y Torricelli, cambió de manera radical
el punto de vista de la ciencia. Evangelista Torricelli, discípulo de Galileo,
fue quien demostró que el aire es un fluido gaseoso que nos rodea, nos envuelve
y nos presiona. Su aporte fue muy importante ya que muchos fenómenos que
ocurrían en la naturaleza, hasta entonces extraños, eran derivados simplemente
de la presión atmosférica.
¿Qué hizo Torricelli? Llenó un tubo con mercurio,
lo invirtió y sumergió la parte abierta en un recipiente con más mercurio. El
nivel de éste en el tubo descendió algunos centímetros, lo que dio lugar en el
extremo cerrado a un espacio sin mercurio, que no podía estar sino vacío. Al
principio muchos hombres de ciencia de la época se negaron a aceptar la teoría
de Torricelli, verificada por el barómetro que él mismo había construido. Tuvo
que transcurrir un tiempo para que la sociedad reconociera que por sobre la
columna de mercurio operaba el propio peso de la atmósfera que rodea la Tierra.
Las experiencias de Torricelli fueron conocidas en
Francia a través de su correspondencia con el religioso Marín Mersenne, quien a su vez estaba en contacto con otros
investigadores que se sintieron entusiasmados a seguir explorando el fenómeno
del espacio vacío. Así fue como el físico Blaise Pascal (1623-1662), en
Francia, reveló las variaciones de la presión atmosférica según las condiciones
climáticas y la altura. A su vez Robert Boyle
(1627-1691), en Inglaterra, llevó a cabo diversos estudios sobre la elasticidad
del aire.
La carrera por perfeccionar los instrumentos que se
usan para conocer el macro y microcosmos continúa hasta la actualidad. Hoy, al
escuchar las noticias meteorológicas sabemos que las altas y bajas presiones
sobre determinadas zonas del planeta tienen una influencia muy importante sobre
el estado del tiempo y gran parte se la debemos a Torricelli, el físico
italiano.
ISAAC BARROW

Isaac Barrow (1630-1677), teólogo y matemático
inglés cuyos métodos matemáticos eran muy próximos a los del cálculo. Está
considerado como uno de los matemáticos más relevantes de su tiempo, sobre todo
en geometría.
Nacido en Londres, Inglaterra, estudió en la
Universidad de Oxford, donde se licenció en Humanidades en 1652. En 1655 inició
un viaje por Europa y Asia Menor, y a su regreso en 1659 fue ordenado ministro
de la Iglesia anglicana.
En 1663 obtuvo el nombramiento de profesor de la
Universidad de Cambridge, cargo que mantuvo hasta 1669, año en que renunció en
favor de su discípulo más distinguido, Isaac Newton. Durante su estancia en
Cambridge, preparó las tres series de conferencias que contienen la mayor parte
de sus contribuciones al estudio de las matemáticas. Sus Lecciones de
geometría (1669-1670)
contienen ideas similares a las que Newton y otros utilizaron más tarde en el
cálculo diferencial e integral. Sus teorías establecen geométricamente la
relación inversa que existe entre el cálculo de tangentes y el de áreas, que
constituye en la actualidad el teorema fundamental del cálculo.
Por mandato real se le nombró en 1670 doctor en
Teología y dos años más tarde director del Trinity College
de Cambridge. En 1663 fue elegido miembro de la Sociedad Real, una organización
independiente dedicada a la promoción de las ciencias naturales; contribuyó de
forma regular en Philosophical Transactions (Actas filosóficas), la revista de
esta Sociedad.
Otras de sus obras son: Elementos de Euclides
(1655), Datos de Euclides (1657), Lecciones de óptica (1669) y Lecciones
de matemáticas (1683).
Además de los trabajos ya mencionados, escribió otros importantes
tratados en matemáticas, pero en
la literatura se dedicó especialmente a escribir sermones, que fueron obras
maestras de argumentaciones elocuentes, donde su tratado Pope's
Supremacy es
considerado como uno de los tratados de controversia más perfectos que existen.
Barrow como hombre fue en todos los aspectos digno de sus grandes talentos,
aunque tuvo una gran vena excéntrica. Murió sin casarse en Londres a la temprana
edad de 47 años.
Ha sido descrito como "bajo de estatura, flaco y de pálido
aspecto", despreocupado en sus vestimentas y un empedernido fumador. Fue
notoria su fuerza y valentía, y se cuenta que una vez cuando viajaba hacia el
Este logró esquivar el ataque de unos piratas gracias a su destreza. Su
predisposición e ingenio le hicieron favorito de Carlos II, quien indujo a sus
cortesanos a respetarle aunque no le mostraran aprecio. Escribía muy a menudo y
con elocuencia, y con su intachable vida y su escrupulosa conciencia fue uno de
los personajes más impresionantes de su tiempo.

Gottfried Wilhelm Leibniz (1646-1716) fue un filósofo, lógico, matemático, jurista,
bibliotecario y político alemán. Fue uno de los grandes pensadores de los
siglos XVII y XVIII, y se le reconoce como "El último genio
universal". Realizó profundas e importantes contribuciones en las áreas de
metafísica, epistemología, lógica, filosofía de la religión, así como a la
matemática, física, geología, jurisprudencia e historia.
Ocupa un lugar igualmente importante tanto en la
historia de la filosofía como en la de las matemáticas. Una de las
contribuciones más importantes de Leibniz a las matemáticas consistió en enunciar
en 1675 los principios fundamentales del cálculo infinitesimal. De acuerdo con
los cuadernos de Leibniz, el 11 de noviembre de 1675 tuvo lugar un
acontecimiento fundamental, ese día empleó por primera vez el cálculo integral
para encontrar el área bajo la curva de una función. Esta aportación se produjo
con independencia de los descubrimientos del científico inglés Isaac Newton,
cuyo sistema de cálculo fue inventado en 1666. El sistema de Leibniz fue
publicado en 1684, el de Newton en 1687, y el método de notación ideado por
Leibniz fue adoptado universalmente y su notación es la que se emplea desde
entonces. Desde 1711 hasta su muerte, la vida de Leibniz estuvo emponzoñada con
una larga disputa con John Keill, Newton y otros
sobre si había inventado el cálculo independientemente de Newton, o si
meramente había inventado otra notación para las ideas de Newton. Leibniz pasó
entonces el resto de su vida tratando de demostrar que no había plagiado las
ideas de Newton.
Leibniz introdujo varias notaciones del cálculo usadas en la
actualidad, por ejemplo, el signo “integral” ∫, que representa una S alargada, derivado del latín summa,
y la letra "d" para referirse a los “diferenciales”, del latín differentia.
Esta ingeniosa y sugerente notación para el cálculo es probablemente su legado
matemático más perdurable. Leibniz no publicó nada acerca de su Calculus hasta 1684. La regla
del producto del cálculo
diferencial es aún denominada “regla de Leibniz para la derivación de un
producto”. Además, el teorema que dice cuándo y cómo diferenciar bajo el
símbolo integral, se llama la “regla de Leibniz para la derivación de una
integral”. Actualmente se emplea la notación del cálculo creada por Leibniz, no
la de Newton.
También inventó el sistema binario, fundamento de
virtualmente todas las arquitecturas de las computadoras actuales. En 1672
inventó una máquina de calcular capaz de multiplicar, dividir y extraer raíces
cuadradas.

Aunque la noción matemática de función estaba
implícita en la trigonometría y las tablas logarítmicas, las cuales ya existían
en sus tiempos, Leibniz fue el primero, en 1692 y 1694, en emplearlas
explícitamente para denotar alguno de los conceptos geométricos derivados de
una curva, tales como abscisa, ordenada, tangente, cuerda y perpendicular. En
el siglo XVIII, el concepto de "función" perdió estas asociaciones
meramente geométricas.
Leibniz fue el primero en ver que los coeficientes
de un sistema de ecuaciones lineales podían ser organizados en un arreglo,
ahora conocido como matriz, el cual podía ser manipulado para encontrar, si
existe, la solución del sistema. Este método fue conocido más tarde como
"Eliminación Gaussiana". Leibniz también hizo aportes en el campo del
álgebra booleana, la lógica simbólica y en las series infinitas.
ISAAC NEWTON
Isaac Newton (1643-1727) fue un físico, filósofo, teólogo,
inventor, alquimista y matemático inglés. Nació el 25 de diciembre
de 1642 (según el calendario juliano vigente entonces; que corresponde al 4 de
enero de 1643, según el calendario gregoriano vigente en la actualidad), en Woolsthorpe, Lincolnshire. Muere en el municipio de Kensington,
Londres, Inglaterra el 20 de marzo de 1727 según el calendario
juliano que corresponde al 31 de marzo de 1727 según el calendario gregoriano.
Sus padres fueron Isaac Newton y Hannah Ayscough, dos campesinos puritanos. No llegó a conocer a su
padre, pues había muerto en octubre de 1642. Cuando su madre volvió a casarse
con Barnabás Smith, este no tenía intención de cargar
con un niño ajeno de tres años, lo dejó a cargo de su abuela, con quien vivió
hasta la muerte de su padrastro en 1653. Este fue posiblemente un hecho
traumático para Isaac; constituía la pérdida de la madre no habiendo conocido
al padre. A su abuela nunca le dedicó un recuerdo cariñoso y hasta su muerte
pasó desapercibida. Lo mismo ocurrió con el abuelo, que pareció no existir
hasta que se descubrió que también estaba presente en la casa y correspondió al
afecto de Newton de la misma forma: lo desheredó.
Cuando Barnabás Smith falleció,
su madre regresó al hogar familiar acompañada por dos hijos de éste matrimonio,
sus hermanastros, pero la unión familiar duró menos de dos años. Isaac fue
enviado a estudiar al colegio The King's
School, en Grantham, a la
edad de doce años. Lo que se sabe de esta etapa es que estudió latín, algo
de griego y lo básico de geometría y aritmética. Era el programa habitual de
estudio de una escuela primaria en ese entonces. Su maestro fue Sr. Stokes, que
tenía buen prestigio como educador.
A los dieciocho años ingresó en la Universidad de
Cambridge para continuar sus estudios. Newton nunca asistió regularmente a
sus clases, ya que su principal interés era la biblioteca. Se graduó en el Trinity
College como un estudiante mediocre debido a su
formación principalmente autodidacta, leyendo algunos de los libros más
importantes de matemática y filosofía natural de la época.
En 1663 Newton leyó la Clavis mathematicae de William Oughtred,
la Geometría de Descartes,
la Óptica de Kepler, la Opera mathematica de Viète, editadas por Frans
van Schooten y en 1664, la Aritmética de
John Wallis, que le serviría como introducción a sus investigaciones sobre
las series infinitas, el teorema del binomio y ciertas cuadraturas.
En 1663 conoció a Isaac Barrow, quien le dio clases de
matemática. En la misma época entró en contacto con los trabajos
de Galileo, Fermat, Huygens y otros, a partir, probablemente, de
la edición de 1659 de la Geometría, de Descartes por Van Schooten. Newton superó rápidamente a Barrow, quien
solicitaba su ayuda frecuentemente en problemas matemáticos.
En esta época la geometría y la óptica ya tenían
un papel esencial en la vida de Newton. Fue en este momento que su fama comenzó
a crecer, ya que inició una correspondencia con la Royal Society. Newton les envió algunos de sus descubrimientos y
un telescopio que suscitó gran interés entre los miembros de la
Sociedad, aunque también las críticas de algunos, principalmente Robert
Hooke. Este fue el comienzo de una de las muchas disputas que tuvo en su
carrera científica. Se considera que Newton mostró agresividad ante sus
contrincantes, que fueron principalmente (pero no únicamente) Hooke, Leibniz y,
en lo religioso, la Iglesia católica. Como presidente de la Royal Society, fue descrito como un dictador cruel, vengativo y
buscapleitos. Sin embargo, fue una carta de Hooke, en la que éste comentaba sus
ideas intuitivas acerca de la gravedad, la que hizo que iniciara de lleno sus
estudios sobre la mecánica y la gravedad. Newton resolvió el
problema con el que Hooke no había podido y sus resultados los escribió en lo
que muchos científicos creen que es el libro más importante de la historia de
la ciencia, Philosophiae naturalis principia mathematica.
En 1693 sufrió una gran crisis psíquica, causante de
largos periodos en los que permaneció aislado, durante los que no comía ni
dormía. En esta época sufrió depresión y arranques de paranoia.
Mantuvo correspondencia con su amigo, el filósofo John Locke, en la que
además de contarle su mal estado, lo acusó en varias ocasiones de cosas que
nunca hizo. Algunos historiadores creen que la crisis fue causada por la
ruptura de su relación con su discípulo Nicolás Fatio
de Duillier. Sin embargo, tras la publicación en 1979
de un estudio que demostró una concentración de mercurio (altamente
neurotóxico) quince veces mayor que la normal en el cabello de Newton, la
mayoría opina que en esta época Newton se había envenenado al hacer sus
experimentos de alquimia, lo que explicaría su enfermedad y los cambios en
su conducta. Después de escribir los Principia abandonó Cambridge,
mudándose a Londres, donde ocupó diferentes puestos públicos de prestigio,
siendo nombrado Preboste del Rey, magistrado de Charterhouse
y director de la Casa de Moneda.
Entre sus intereses más profundos se encontraban
la alquimia y la religión, temas en los que sus escritos sobrepasan
con mucho en volumen a sus escritos científicos. Entre sus opiniones religiosas
defendía el arrianismo y estaba convencido de que las Sagradas
Escrituras habían sido violadas para sustentar la
doctrina trinitaria. Esto le causó graves problemas al formar parte del
Trinity College en Cambridge y sus ideas religiosas
impidieron que pudiera ser director del College.
Entre sus estudios alquímicos se encontraban temas esotéricos como la
transmutación de los elementos, la piedra filosofal y el elixir de la
vida.
Desde finales de 1664 trabajó intensamente en diferentes
problemas matemáticos. Abordó entonces el teorema del binomio, a
partir de los trabajos de John Wallis, y desarrolló un método propio
denominado cálculo de fluxiones. Poco después regresó a la granja familiar
a causa de una epidemia de peste bubónica.
Retirado con su familia durante los
años 1665 y 1666, conoció un período muy intenso de
descubrimientos, entre los que destaca la ley del inverso del cuadrado de
la gravitación, su desarrollo de las bases de la mecánica clásica, la
formalización del método de fluxiones y la generalización del teorema del
binomio, poniendo además de manifiesto la naturaleza física de los colores. Sin
embargo, guardaría silencio durante mucho tiempo sobre sus descubrimientos ante
el temor a las críticas y al robo de sus ideas. En 1667 reanudó sus estudios en
la Universidad de Cambridge.
De 1667 a 1669 emprendió investigaciones sobre óptica y
fue eligido fellow del Trinity
College. En 1669, su mentor, Isaac Barrow,
renunció a su Cátedra Lucasiana de
matemática, puesto en el que Newton le sucedería hasta 1696. El mismo año envió
a John Collins, por medio de Barrow, su Analysis
per aequationes número terminorum
infinitos. Para Newton, este manuscrito representa la introducción a un
potente método general, que desarrollaría más tarde: su cálculo
diferencial e integral.
Newton había descubierto los principios de su cálculo
diferencial e integral hacia 1665-1666 y, durante el decenio
siguiente, elaboró al menos tres enfoques diferentes de su nuevo análisis.
Newton y Leibniz protagonizaron una agria polémica sobre
la autoría del desarrollo de esta rama de la matemática. Los historiadores de
la ciencia consideran que ambos desarrollaron el cálculo independientemente, si
bien la notación de Leibniz era mejor y la formulación de Newton se aplicaba
mejor a problemas prácticos. La polémica dividió aún más a los matemáticos
británicos y continentales. Newton utilizó su cargo de presidente de la Royal Society para que se formara una comisión que investigara el
tema, y él, en secreto, escribió el informe de la comisión que hacía a Leibniz
responsable del plagio. Newton incluso recopiló la relación de acusaciones que
esta institución había publicado. Los efectos de la disputa se alargaron casi
hasta su muerte.
Newton abordó el desarrollo del cálculo a partir de
la geometría analítica desarrollando un enfoque geométrico y analítico
de las derivadas matemáticas aplicadas sobre curvas definidas a través
de ecuaciones. Newton también buscaba cómo cuadrar distintas curvas, y la
relación entre la cuadratura y la teoría de tangentes. Después de los
estudios de Roberval, Newton se percató de que
el método de tangentes podía utilizarse para obtener las velocidades
instantáneas de una trayectoria conocida. En sus primeras investigaciones
Newton lidia únicamente con problemas geométricos, como encontrar tangentes,
curvaturas y áreas utilizando como base matemática la geometría
analítica de Descartes. No obstante, con el afán de separar su teoría
de la de Descartes, comenzó a trabajar únicamente con las ecuaciones y sus
variables sin necesidad de recurrir al sistema cartesiano.
Después de 1666 Newton abandonó sus trabajos matemáticos,
sintiéndose interesado cada vez más por el estudio de la naturaleza y
la creación de sus Principia.
En 1687, Newton publicó sus Principios matemáticos
de la filosofía natural. Editados 22 años después de la Micrographia de Hooke, describían las leyes del
movimiento, entre ellas la ley de la gravedad. Pero lo cierto es que, como
indica Allan Chapman, Robert Hooke «había formulado antes que
Newton muchos de los fundamentos de la teoría de la gravitación». La labor de
Hooke también estimuló las investigaciones de Newton sobre la naturaleza de la
luz.
Por desgracia, las disputas en materia
de óptica y gravitación agriaron las relaciones entre ambos hombres.
Newton llegó al extremo de eliminar de sus Principios matemáticos toda
referencia a Hooke. Un especialista asegura que también intentó borrar de los
registros las contribuciones que éste había hecho a la ciencia. Además, los
instrumentos de Hooke —muchos elaborados artesanalmente—, buena parte de sus
ensayos y el único retrato auténtico suyo se esfumaron una vez que Newton se
convirtió en presidente de la Sociedad Real. A consecuencia de lo anterior, la
fama de Hooke cayó en el olvido, un olvido que duraría más de dos siglos, al
punto que no se sabe hoy día dónde se halla su tumba.

Michel Rolle (1652-1719) fue un matemático francés
nacido en Ambert. Se dedicó principalmente a la
teoría de ecuaciones, dominio en el que encontró diversos resultados, entre los
que destaca el reconocido teorema que lleva su nombre formulado
en 1691. En el cual representa una aplicación de la teoría de funciones a
la de ecuaciones algebraicas.
Michel Rolle fue hijo de un encargado de una tienda, tuvo
dificultades para asistir a la escuela más allá de la primaria, aunque desde
muy joven consiguió trabajos como escribano para algunos notarios y abogados. A
los 24 años viajó a Paris, donde consiguió trabajo como secretario y contador.
Sus habilidades matemáticas le permitieron ser exitoso en
su trabajo y siempre tuvo tiempo suficiente para estudiar por su cuenta
matemáticas. Estudió el trabajo de Diofanto,
además de que siguió el trabajo de sus paisanos contemporáneos Bachet de Meziriac y Jacques
Ozanam. Este último, también autodidacta, fue un
apasionado de las matemáticas recreativas y frecuentemente publicaba acertijos
y curiosidades matemáticas muy populares en Francia.
En 1682, Rolle publicó la solución de un problema
propuesto por Ozanam: Encontrar cuatro
números tales que la diferencia entre cada dos de ellos es tanto la suma de los
primeros tres como un cuadrado perfecto. La solución de Rolle fue
calificada de “elegante” y le dio fama entre los círculos de entusiastas
matemáticos. Jean-Baptiste Colbert, en ese
entonces Contralor General de Finanzas, otorgó a Rolle una beca como premio a
su publicación. El Marqués de Louvois, Ministro
de Guerra, lo contrató como tutor para su hijo, además de ofrecerle un puesto
administrativo en el ministerio.
Rolle fue admitido como miembro de la Academia Real
de Ciencias en 1685. En 1690 publicó el libro Traite d’algebre, que comprende sus estudios en la teoría de
ecuaciones. En él, aparece su “método de las cascadas”, el cual le permite
estudiar raíces distintas de la ecuación ![]() . Un año más tarde
publica Demonstration d’une Methode pour
resoudre les Egalitez de tous les degrez, en donde
explica con más detalle su método, además de contener las demostraciones
completas de sus resultados, las cuales faltaban en el Traite d’algebre.
. Un año más tarde
publica Demonstration d’une Methode pour
resoudre les Egalitez de tous les degrez, en donde
explica con más detalle su método, además de contener las demostraciones
completas de sus resultados, las cuales faltaban en el Traite d’algebre.
En 1699 Rolle recibió la Pensión de Geometría de
la Academia, lo cual le permitió dedicarse por completo a las matemáticas. Para
ese entonces publicó Methode pour resoudre les equations indeterminees de l’algebre, en donde continúa sus estudios de ecuaciones
algebraicas. Paradójicamente, Rolle dedicó buena parte de sus trabajos en
criticar duramente las nuevas técnicas del cálculo infinitesimal, dudando la
validez de los métodos, basados en tomar “límites de cocientes entre 0″.
Rolle sí terminó por aceptar la validez y utilidad del cálculo infinitesimal,
aunque nunca se enteró que su teorema se convertiría en uno de los principales
pilares del cálculo diferencial.
JOHANN BERNOULLI

Johann Bernoulli (1667-1748), también conocido
como Jean o John fue un matemático, médico y filólogo suizo,
nacido en Basilea.
Su padre de religión calvinista deseaba que su
hijo se convirtiera en comerciante y aceptó entrar como aprendiz en el negocio
familiar de especias y medicinas, pero terminó por hacerlo tan mal que su
contrariado padre se vio obligado a rectificar su orientación originaria,
entonces su padre decidió que se convirtiera en médico, profesión también
relacionada con el negocio familiar. En 1683 ingresa en la Universidad de
Basilea y saca el título de médico; sin embargo, durante este tiempo junto a su
hermano Jakob también se dedicó a aprender el lenguaje de los
números.
Johann Bernoulli
fue todavía más prolífico que su hermano en el campo de la Matemática y
difundió el Cálculo en Europa. Sus estudios abarcan la Física, la Química y la
Astronomía, además de la Matemática. En las ciencias aplicadas Johann Bernoulli contribuyó notablemente a
los estudios de la óptica, escribió sobre la teoría de las mareas y sobre la
teoría matemática de las velas de los barcos. Enunció el principio de los
desplazamientos virtuales en la mecánica.
Johann fue un hombre de extraordinario vigor físico e
intelectual, permaneciendo activo hasta pocos días antes de su muerte a la edad
de 80 años. Las novedades matemáticas de Leibniz sobre el cálculo
infinitesimal cautivaron a ambos hermanos. En 1691 viaja a París para
guiar a los matemáticos franceses en el uso del cálculo entre los cuales se
hallaba el marqués de Guillaume de L' Hôpital,
quien lo tuvo por mentor con buenos honorarios.
En Francia se convirtió en defensor de Leibniz en la
polémica que mantenía con Isaac Newton, por deslindar quién había sido el
primero en enunciar los principios del cálculo infinitesimal. En 1695 el
científico holandés Christiaan Huygens le
invita a convertirse en presidente del departamento de matemáticas de la
Universidad de Groninga. En 1705, tras la muerte de su hermano por
tuberculosis, le sustituyó como catedrático de matemáticas en la Universidad
de Basilea, donde permaneció durante 42 años como profesor, allí tuvo como
discípulos a Johann Samuel König y Leonhard Euler. Se centró en el cálculo infinitesimal y
resolvió la ecuación diferencial de Bernoulli, propuesta por su hermano.
Sus hijos Nicolau, Daniel y Johann Bernoulli fueron
grandes matemáticos.

Brook
Taylor (1685-1731)
fue un matemático inglés. Hijo de John Taylor, del Parlamento de Bifrons y de Olivia Tempest (hija
de Sir Nicholas Tempest). Entró en la Universidad
de St. John de Cambridge como estudiante en 1701. Se licenció en
Derecho en 1709 y se doctoró en 1714. Estudió matemáticas con John Machin y John Keill.
En 1708 encontró una importante solución del problema del
"centro de oscilación" que publicó hasta mayo de 1714 ("Phylosophycal Transactions of the Royal Society" vol.28),
lo que provocó una disputa sobre su autoría con Johann Bernoulli.
En su Methodus Incrementorum Directa et Inversa (Londres, 1715)
desarrolló una nueva parte dentro de la investigación matemática, que hoy se
llama cálculo de las diferencias finitas. Entre las distintas
aplicaciones, se usó para determinar la forma del movimiento de una cuerda
vibrante, reducido por él por vez primera con éxito a principios mecánicos. El
mismo trabajo contenía la famosa fórmula conocida como Teorema de Taylor,
cuya importancia sólo se reconoció en 1772, cuando Lagrange se dio cuenta de su valor y lo definió como
"el diferencial principal del fundamento del cálculo".
En su Ensayo sobre la perspectiva lineal (Londres, 1715)
Taylor expresó los verdaderos principios de la perspectiva de modo más original
y general que los anteriores; pero el trabajo tuvo algún problema por su
brevedad y su oscuridad, defectos que se pueden aplicar a la mayor parte de sus
obras; este trabajo necesitó el perfeccionamiento que desarrolló Joshua Kirby (1754).
Taylor fue elegido miembro de la Royal Society a principios de 1712 y el mismo año
pasó a formar parte del comité para el juicio sobre reclamos de Sir Isaac
Newton y Gottfried Leibniz; desde el 13 de enero de 1714 al 21
de octubre a 1718 fue secretario de la sociedad. Desde 1715 sus
estudios dan un giro filosófico y religioso. A partir de este año mantuvo
correspondencia con Pierre Rémond de Montmort sobre las doctrinas de Nicolás Malebranche; a raíz de ello, se encontró entre sus cartas y
tratados inacabados, tratados Sobre los sacrificios hebreos y Sobre
la legitimidad de comer sangre, escritos por él a su regreso de Aquisgrán en1719.
Su matrimonio en 1721 con una dama de Wallington, Surrey le enemistó con su padre, que
acabó en 1723 tras la muerte de su mujer durante el parto, en el que
también murió el niño. Los dos años siguientes los pasó con su familia en Bifrons; en 1725 se casó, esta vez con la
aprobación de su padre, con Sabetta Sawbridge de Olantigh, que
también murió de parto en 1730; en esta ocasión, sin embargo, su hija
sobrevivió. Su frágil salud hizo que su estado degenerara con rapidez y murió.
Desde la muerte de su padre (1729) había heredado la propiedad de Bifrons. Como matemático, era el único inglés tras Isaac
Newton y Roger Cotes capaz de competir con matemáticos
como Johann Bernoulli. Sin embargo, gran parte de los resultados de su
demostración no tuvieron repercusión o se perdieron a causa de su incapacidad
de expresar sus ideas completamente y con claridad.
Un trabajo póstumo titulado Contemplatio
Philosophica fue impreso en 1793 por
su sobrino, Sir William Young, que tenía un prólogo sobre la vida del autor y
las cartas recibidas por Bolingbroke, Bossuet. Muchos de sus artículos breves se publicaron en la
"Phylosophycal Transactions
of the Royal Society",
volúmenes del 27 al 33, incluyendo los informes de algunos experimentos
interesantes sobre el magnetismo y sobre la atracción del vaso
capilar. Publicó en 1719 una versión mejorada de su trabajo sobre la
prospectiva, con el título Nuevos principios de la prospectiva lineal,
revisada por Colson en 1749, e impresa con el
retrato y la biografía del autor en 1811.
Taylor en su obra Methodus
Incrementorum hizo una primera aproximación
completa sobre la refracción astronómica.
En 1715, Taylor encuentra que el movimiento de un punto
arbitrario de la cuerda es el de un péndulo simple y determina su tiempo de
vibración (periodo). Obtiene en su lenguaje propio, un tanto distinto del
nuestro, la ecuación diferencial de la cuerda vibrante, es decir, la ecuación
unidimensional de ondas y a partir de ella halla una solución: la forma de la
curva que toma la cuerda en un instante dado es sinusoidal.

Colin Maclaurin
(1698-1746) matemático escocés. Ingresó en la universidad a la edad de 11 años,
fue profesor en la universidad de Aberdeen a los 19 y posteriormente en la de
Edimburgo. Expuso un original método de generación de las cónicas en su
obra Geometría orgánica (1720) y sentó las bases para una
fundamentación lógica del cálculo infinitesimal en el Tratado de las
fluxiones (1742). En su Tratado de álgebra (1748)
aplicó el método de los determinantes a la resolución de ecuaciones con cuatro
incógnitas. Dos años después este método fue popularizado por Gabriel Cramer como Regla de Cramer.
Maclaurin era hijo de un eclesiástico escocés,
de quien heredó un espíritu ardientemente religioso próximo a la beatería.
Matriculado en la Universidad de Glasgow, reveló un talento muy precoz para las
matemáticas; en 1717, a los diecinueve años, fue ya nombrado profesor de tal
materia en Aberdeen. Dos años después su gran notoriedad le llevó a la Royal Society. Precisamente entonces publicó Geometría
orgánica (1720), texto que puede considerarse entre las más
importantes de sus obras de matemáticas y que contiene un original método de
generación de las cónicas; de tal libro ofreció luego en Philosophical Transactions
(1735) un interesante apéndice.
En 1722, durante un viaje por Francia, escribió un ensayo
de mecánica racional sobre la percusión de los cuerpos que obtuvo el premio de
1724 de la Académie des Sciences.
De vuelta en Inglaterra, buscó una colocación que le diera un desahogo
económico mayor que el procedente de la modesta cátedra del colegio de
Aberdeen. En tal aspecto le ayudó mucho la amistad de Newton. Semejante a
él en ideas políticas y religiosas (ambos eran "tories" y
protestantes moderados), Colin Maclaurin,
como casi todos los grandes hombres de ciencia de los primeros años del siglo
XVIII inglés, se mostraba ferviente newtoniano; a la memoria del amigo y
maestro dedicaría luego la Exposición de los descubrimientos
filosóficos de Newton, uno de los mejores documentos del newtonianismo de la primera generación.
Apoyó también a Newton y su filosofía contra los ataques
de Berkeley en el Tratado sobre las fluxiones. Newton recomendó
vivamente a Maclaurin para la cátedra de matemáticas
de la Universidad de Edimburgo y ofreció incluso completar su estipendio con
una aportación personal. En 1725 el candidato ocupó el puesto en cuestión y en
adelante dedicó su vida a la enseñanza y a la investigación científica.
En 1740 compartió con Leonhard
Euler y Daniel Bernoulli el premio ofrecido por la Académie
des Sciences de París a un ensayo sobre las mareas.
El año anterior y a instancia suya, la Sociedad Médica de Edimburgo se había
transformado en Philosophical Society,
con lo cual amplió su campo de acción, según el modelo de la Royal Society londinense. Un solo episodio perturbó la existencia
pacífica de este piadoso matemático escocés. En 1745, los rebeldes
desembarcados en Escocia con el pretendiente Jacobo Stuart se dirigieron contra
Edimburgo; Maclaurin, fiel a sus ideas políticas y
religiosas, se manifestó partidario de la monarquía de los Hannover y participó
activamente en la defensa de la ciudad, a cuya caída hubo de huir a Inglaterra
para eludir el acto de sumisión.
De los trabajos citados, la obra principal de Colin Maclaurin es sin duda la
conocida como Tratado de las fluxiones (su título original
es A Complete System of Fluxions;
with their Application to the most Considerable Problems in Geometry and Natural Philosophy),
publicada en Edimburgo, en dos volúmenes, en 1742. En la época en que fue
impresa esta obra los nuevos procedimientos del cálculo infinitesimal habían
recibido un gran desarrollo, debido especialmente a la obra de B. Cavalieri, de Newton, de Leibniz y de sus inmediatos
sucesores, los cuales; sin embargo, se habían preocupado más de extender los
confines del nuevo dominio matemático que de consolidar sus principios y de
reforzar su consistencia lógica.
El libro de Maclaurin quiere
superar la laguna que resultaba de ello, fortaleciendo la nueva doctrina con
rigurosas demostraciones; aporta a esta obra la solución de muchos nuevos
problemas de geometría, de mecánica, de astronomía, y especialmente una
investigación sobre la atracción ejercida por un elipsoide sobre un punto
situado en su superficie, o en su interior, cuestión de la que ya se había
ocupado con anterioridad en una Memoria acerca del flujo y reflujo del
mar.
Lagrange juzga esta parte de la obra como
"una obra maestra de geometría, sólo comparable a lo más bello e ingenioso
que el propio Arquímedes ha dejado". Maclaurin
parte de un nuevo teorema relativo a las cuerdas de dos elipses concéntricas y,
mediante tal proposición, logra demostrar el teorema fundamental que Newton
habla admitido sin una verdadera comprobación: "una masa fluida homogénea,
girando alrededor de un eje que pase por su centro de gravedad, debe adoptar la
figura de un elipsoide de revolución, supuesto que todas sus moléculas se
atraigan en razón directa a sus masas o en razón inversa al cuadrado de sus
distancias".
El nuevo método de Maclaurin
pareció tan interesante a Clairaut que le indujo a
abandonar el método puramente analítico que había seguido hasta entonces para
demostrar la forma de la Tierra. En cuanto al caso de un punto
"exterior" al elipsoide, el problema era mucho más difícil. El
célebre geómetra escocés apenas lo abordó; habían de tratarlo más tarde con
mayor amplitud Legendre e Ivory.
LEONHARD EULER

Leonhard Paul Euler (1707-1783), conocido como Leonhard Euler, fue un matemático y físico suizo. Se trata
del principal matemático del siglo XVIII y uno de los más grandes y prolíficos
de todos los tiempos.
Euler nació en Basilea hijo de Paul Euler, un pastor
calvinista, y de Marguerite Brucker,
hija de otro pastor. Tuvo dos hermanas pequeñas llamadas Anna María y María
Magdalena. A la edad de 13 años se matriculó en la Universidad de Basilea donde
estudió con el matemático suizo Johann Bernoulli, en 1723 recibió el título de
maestro de Filosofía, licenciándose a los 16 años y en 1726, a los 19 años de
edad, Euler finalizó su Doctorado con una tesis sobre la propagación del sonido
bajo el título “De Sono”. En 1727, por invitación de la emperatriz de
Rusia Catalina I, fue miembro del profesorado de la Academia de Ciencias de San
Petersburgo. Fue nombrado catedrático de física en 1730 y de matemáticas en
1733. En 1741 fue profesor de matemáticas en la Academia de Ciencias de Berlín
a petición del rey de Prusia, Federico el Grande. Euler regresó a San
Petersburgo en 1766, donde permaneció hasta su muerte.
La vista de Euler fue empeorando a lo largo de su vida. En
el año 1735 Euler sufrió una fiebre casi fatal, y tres años después de dicho
acontecimiento quedó casi ciego de su ojo derecho. Euler, sin embargo, prefería
acusar de este hecho al trabajo de cartografía que realizaba para la Academia
de San Petersburgo. La vista de ese ojo empeoró a lo largo de su estancia en
Alemania. Euler más tarde sufrió cataratas en su ojo sano, el izquierdo, lo que
le dejó prácticamente ciego pocas semanas después de su diagnóstico. A pesar de
ello, parece que sus problemas de visión no afectaron a su productividad
intelectual, dado que lo compensó con su gran capacidad de cálculo mental y su
memoria fotográfica. Por ejemplo, Euler era capaz de repetir la Eneida de
Virgilio desde el comienzo hasta el final y sin dudar en ningún momento, y en
cada página de la edición era capaz de indicar qué línea era la primera y cuál
era la última. También se sabía de memoria las fórmulas de trigonometría y las
primeras 6 potencias de los primeros 100 números primos.
Pasó los últimos años de su vida prácticamente ciego, pero
siguió trabajando. Muchos trabajos se los dictó a su hijo mayor. Esto
incrementó el respeto que la comunidad científica ya tenía por él. Ha sido uno
de los matemáticos más prolíficos de la historia. Su actividad de publicación
fue incesante (un promedio de 800 páginas de artículos al año en su época de
mayor producción, entre 1727 y 1783), Euler produjo numerosas obras matemáticas
importantes, así como reseñas matemáticas y científicas. Se le considera el ser
humano con mayor número de trabajos y artículos en cualquier campo del saber,
sólo equiparable a Gauss. Se calcula que sus obras completas reunidas podrían
ocupar entre 60 y 80 volúmenes. Una afirmación atribuida a Pierre Simon Laplace expresa la influencia de Euler en los
matemáticos posteriores: “Lean a Euler, lean a Euler, él es el maestro de todos
nosotros”.
En su libro Introducción al análisis de los infinitos
(1748), Euler realizó el primer tratamiento analítico completo del álgebra, la
teoría de ecuaciones, la trigonometría y la geometría analítica. En esta obra
trató el desarrollo de series de funciones y formuló la regla por la que sólo
las series convergentes infinitas pueden ser evaluadas adecuadamente. También
abordó las superficies tridimensionales y demostró que las secciones cónicas se
representan mediante la ecuación general de segundo grado en dos dimensiones.
Otras obras trataban del cálculo (incluido el cálculo de variaciones), la
teoría de números, números imaginarios y álgebra determinada e indeterminada.
Euler, aunque principalmente era matemático, realizó también aportaciones a la
astronomía, la mecánica, la óptica y la acústica. Entre sus obras se encuentran
Instituciones del cálculo diferencial (1755), Instituciones del cálculo
integral (1768-1770) e Introducción al álgebra (1770).
Euler introdujo y popularizó varias convenciones
referentes a la notación en los escritos matemáticos en sus numerosos y muy
utilizados libros de texto. Posiblemente lo más notable fue la introducción del
concepto de función matemática, siendo el primero en escribir f(x) para hacer
referencia a la función f aplicada sobre el argumento x. Esta nueva forma de
notación ofrecía más comodidad frente a los rudimentarios métodos del cálculo
infinitesimal existentes hasta la fecha, iniciados por Newton y Leibniz, pero
desarrollados basándose en las matemáticas del último. También introdujo la
notación moderna de las funciones trigonométricas, la letra e como base del
logaritmo natural o neperiano (el número e es conocido también como el número
de Euler), la letra griega Σ como símbolo de los sumatorios y la letra i
para hacer referencia a la unidad imaginaria. El uso de la letra griega π
para hacer referencia al cociente entre la longitud de la circunferencia y la
longitud de su diámetro también fue popularizado por Euler, aunque él no fue el
primero en usar ese símbolo.

Jean le Rond
D'Alembert (1717-1783) fue un matemático, filósofo y
enciclopedista francés, uno de los máximos exponentes del movimiento ilustrado.
Es célebre por crear, con Diderot, L'Encyclopédie y por su labor en el campo de
las matemáticas, relativo a las ecuaciones diferenciales y a las derivadas
parciales.
Hijo ilegítimo de Madame de Tencin
y del caballero Destouches, D'Alembert,
recién nacido, fue abandonado en la puerta de la iglesia de Saint-Jean-le Rond (de ahí el nombre que se le impuso). Fue recogido
luego por Madame Rousseau, mujer de pobre condición, la cual se ocupó de su
crianza. D'Alembert, que en un principio se hizo
llamar Daremberg, nunca fue reconocido por sus
padres, pero Destouches sufragó los gastos de su
educación, que pudo ser tan selecta como la de cualquier hijo de la nobleza.
A los 18 años consiguió el título de bachiller en artes,
después de varios años de estudio en una escuela jansenista. Tras dos años
de estudiar derecho, empezó a cursar la carrera de medicina, que
pronto abandonó.
La gran pasión de D'Alembert
fueron las matemáticas, que había aprendido en forma prácticamente autodidacta;
en 1739, presentó su primer trabajo en la prestigiosa Academia de Ciencias de
París. Dos años después, con tan solo 24 años de edad, fue elegido miembro de
esa Academia.
En 1743 publicó su Tratado de dinámica, obra
fundamental en que formula el conocido principio de D'Alembert,
que confirma la existencia de la inercia en un punto material, como reacción
ejercida por ese punto frente a las fuerzas que actúan sobre él. Con ella, el
joven D'Alembert alcanza de inmediato prestigio en
toda Europa como uno de los pensadores científicos más reputados; Lagrange afirmará que ese tratado «reduce la estática
a la dinámica».D'Alembert siguió elaborando nuevos
trabajos en el campo de la física matemática, entre ellos el titulado Tratado
del equilibrio y del movimiento de los fluidos.
En 1772 se le nombró secretario perpetuo de la
Academia Francesa, escribiendo entonces los Elogios sobre los
académicos fallecidos entre 1700 y 1770. Por todo ello D'Alembert representó un nuevo tipo de
intelectual capaz de compaginar la pertenencia a la nueva red
internacional de instituciones científicas y un ensayismo independiente y
políticamente comprometido.
Muere en París el 29 de octubre de 1783, cuando ya gozaba
de la reputación de ser uno de los pensadores más eminentes de la ilustración
francesa. Se le enterró modestamente. Condorcet,
amigo y sucesor suyo en ciertos terrenos matemáticos, acompañó su cortejo
fúnebre; además lo elogió en la Academia, pues había recibido ese puesto de
manos de D'Alembert.
Abordó la matemática a través de la física,
con el problema de los tres cuerpos (imposibilidad de encontrar
ecuaciones de las trayectorias - inestabilidad del sistema), la precesión de
los equinoccios (razón del deslizamiento de las estaciones), las
cuerdas vibrantes (distintos modos de vibración - aplicación a la música). Esto
le llevó a estudiar las ecuaciones diferenciales y las ecuaciones a
las derivadas parciales. También inventó un criterio para distinguir
una serie convergente de una divergente.
Su obra maestra fue el Tratado de dinámica,
donde enunció el teorema que lleva su nombre (principio de D'Alembert). El Teorema Fundamental del Álgebra recibe,
en algunos países de Europa, el nombre de teorema de D'Alembert - Gauss, dado que D'Alembert
fue el primero en dar una prueba casi completa sobre dicho teorema.

Joseph Louis de Lagrange,
bautizado como Giuseppe Lodovico Lagrangia, (1736-1813), fue
un físico, matemático y astrónomo italiano que después
vivió en Prusia y Francia.
Lagrange trabajó para Federico II de
Prusia, en Berlín, durante veinte años. Lagrange
demostró el teorema del valor medio, desarrolló la mecánica Lagrangiana y tuvo una importante contribución
en astronomía.
Joseph Louis de Lagrange
procedía de una familia parisina que gozaba de buena posición social. Fue
educado en la Universidad de Turín y no fue hasta los diecisiete años
cuando mostró interés por la matemática. Su entusiasmo lo despertó la lectura
de una obra del astrónomo Edmund Halley. Tras un año de incesante trabajo
era ya un matemático consumado.
Cuando tenía sólo diecinueve años envió una carta a Leonhard Euler en que resolvió un problema, que había
sido un asunto de discusión durante más de medio siglo, mediante una nueva
técnica: el cálculo de variaciones. Euler reconoció la generalidad del
método y su superioridad, con una cortesía rara en él retuvo un artículo que él
había escrito previamente para que el joven italiano tuviera tiempo para
completar su trabajo, como exige la invención de un nuevo método de cálculo. El
nombre de esta rama del análisis la sugirió el propio Euler. Este trabajo puso
a Lagrange en primera línea entre los matemáticos de
su época. En 1758, con la ayuda de sus alumnos, Lagrange
publicó en la Academia de Turin la mayoría de sus
primeros escritos, consistentes en los cinco volúmenes normalmente conocidos
como Miscellanea Taurinensia.
En 1761 Lagrange no
tenía rival en el campo de las matemáticas; pero su trabajo incesante durante
los últimos nueve años habían afectado seriamente su salud y los doctores se
negaron a ser responsables de su vida a menos que él se lo tomara en serio.
Aunque su salud fue temporalmente restablecida su sistema nervioso nunca
recuperó su tono y de aquí en adelante padeció constantemente ataques de
melancolía severa.
Lagrange era de mediana estatura, complexión
débil, con ojos azul claro y un color de piel pálido. Era de un carácter
nervioso y tímido, detestó la controversia y al evitarla de buena gana permitió
a otros tener crédito por cosas que él había hecho.
Ya en 1756, Euler, con el apoyo de Maupertuis,
hizo un intento para traer a Lagrange a la academia
de Berlín. Más tarde, D'Alembert intercedió en
favor de Lagrange con Federico de Prusia y
escribió a Lagrange solicitándole dejar Turín por una
posición considerablemente más prestigiosa en Berlín. Lagrange
rechazó ambas ofertas, respondiendo en 1765 que “Me parece que Berlín no
sería nada adecuado para mí mientras M. Euler esté allí”.
En 1766 Euler abandonó Berlín y Federico
II el Grande escribió a Lagrange para expresarle
su deseo de que "el rey más grande de Europa" debería tener "el
matemático más grande de Europa" viviendo en su corte. Lagrange
aceptó la oferta y durante los siguientes veinte años en Prusia, no sólo
produjo la serie más grande de documentos publicada en Berlín, sino que publicó
su trabajo monumental, la Mécanique analytique.
Su estancia en Berlín comenzó con un desafortunado error:
estando la mayoría de sus colegas casados y siguiendo el consejo de las esposas
de ellos, en el sentido de que casarse era la única manera de estar contento,
se casó; su esposa se murió pronto, pero la unión no fue feliz.
Lagrange era el favorito del rey y
frecuentemente disertó sobre las ventajas de una regularidad perfecta en la
vida. La lección la aplicó a su vida y Lagrange
estudió su mente y su cuerpo como si fueran máquinas y encontró experimentando
la cantidad exacta de trabajo que podía hacer sin perder la salud. Todas las
noches se ponía una tarea definida para el próximo día y al completar cualquier
tema escribía un corto análisis para ver qué puntos en las demostraciones eran
susceptibles de mejora. Siempre pensó en sus artículos antes de componerlos y
normalmente los escribió con aseo y sin una sola raspadura o corrección.
En 1786 Federico II murió y Lagrange,
que se había adaptado al clima de Berlín, aceptó alegremente la oferta
de Luis XVI para emigrar a París. Había recibido invitaciones
similares de España y Nápoles. En Francia fue recibido con
distinción y se prepararon apartamentos especiales en el Louvre para su
recepción. Al principio de su residencia tuvo un ataque de melancolía y tuvo
una copia impresa de su Mécanique, en la
que había trabajado un cuarto de siglo, sin abrir en su escritorio durante más
de dos años. La curiosidad acerca de los resultados de la revolución
francesa lo sacó de su letargo, una curiosidad que pronto se volvió en
alarma con el desarrollo de la revolución.
En 1792, la inexplicable tristeza de su vida y su
timidez movió la compasión de una joven muchacha que insistió en casarse siendo
feliz con dicha unión. Aunque el decreto de octubre de 1793 que
exigía que todos los extranjeros dejaran Francia no le fue aplicado, deseaba
marcharse cuando le ofrecieron la presidencia de la comisión para la reforma de
pesos y medidas.
Aunque Lagrange había querido
salir de Francia, nunca estuvo en peligro y los diferentes gobiernos
revolucionarios (y más tarde, Napoleón) le cubrieron de honores y
distinciones. En 1794 Lagrange fue nombrado
profesor de la École polytechnique y
las conferencias que dio allí, a los matemáticos que tuvieron la suerte de
poder asistir a ellas, tenían su base en su Théorie
des fonctions analytiques.
En 1795 Lagrange ocupó
una silla matemática honorífica en la École normale que disfrutó sólo durante cuatro meses, ya que
la école fue cerrada. Sus conferencias aquí eran
bastante elementales y no contienen nada de importancia especial.
En 1810 Lagrange
comenzó una revisión completa de la Mécanique
analytique, pero sólo pudo completar unos dos
tercios antes de su muerte en 1813.
En 1758, con ayuda de sus alumnos, Lagrange
fundó una sociedad que, más tarde, se denominó la Academia Turinesa de
Ciencias. La mayor parte de sus primeros trabajos se encuentran en los cinco
volúmenes de los registros de la Academia, conocidos usualmente como Miscellanea Taurinensia. Muchos
de estos trabajos son publicaciones elaboradas.
Su actividad mental durante estos veinte años
en Prusia fue asombrosa, no sólo por el hecho de producir su
espléndida Mécanique analytique, sino por contribuir, con doscientos
trabajos, a las Academias de Berlín, Turin, y París.
Algunos de éstos realmente son tratados y todos, sin excepción, son de una
extraordinaria calidad. Salvo un corto tiempo cuando él estaba enfermo en que
produjo aproximadamente un artículo al mes.
Entre 1772 y 1788, Lagrange
reformuló la mecánica clásica de Isaac Newton para simplificar
fórmulas y facilitar los cálculos. Esta mecánica se llama mecánica Lagrangiana y origen de la mecánica analítica. Escribe
su monumental «Tratado de Mecánica Analítica». En este tratado recoge, completa
y unifica los conocimientos desde Newton. Este libro, para sus contemporáneos
una referencia, es una apología de la utilización de las ecuaciones
diferenciales en mecánica. En el libro extiende la ley del trabajo virtual y
hace de ella un principio fundamental y, con la ayuda del cálculo
diferencial, deduce toda la mecánica de sólidos y fluidos.
Hay también numerosos artículos sobre varios puntos
de geometría analítica. En dos de ellos, escritos bastante después,
en 1792 y 1793, redujo las cuádricas a
su forma canónica.
Durante los años
de 1772 a 1785 contribuyó con una larga serie de artículos
que crearon ciencia, las ecuaciones diferenciales, en derivadas parciales.
Una gran parte de estos resultados se reunieron en la segunda edición del
cálculo integral de Euler publicado en 1794.
Durante los últimos años en Francia su trabajo se centró
en el Análisis. Sus conferencias en la École polytechnique trataron del cálculo diferencial, la
base de su Théorie des fonctions analytiques, que se
publicó en 1797.
Este trabajo es la extensión de una idea contenida en un
artículo que él había enviado a Berlín en 1772. Un método algo similar se había
usado previamente por John Landen en el Análisis
residual, publicado en Londres en 1758. Lagrange
creyó que podía librarse así de las dificultades por el uso de cantidades
infinitamente grandes e infinitamente pequeñas, que los filósofos objetaron en
el tratamiento usual del cálculo diferencial.
El libro está dividido en tres partes. La primera da una
prueba algebraica del teorema de Taylor. La segunda trata las aplicaciones
a la geometría; y la tercera aplicación a la mecánica. Otro tratado en las
mismas líneas fue su Leçons sur le calcul des fonctions,
publicado en 1804. Estos trabajos pueden ser considerados como el punto de
arranque para las investigaciones de Cauchy, Jacobi y Weierstrass.
Con posterioridad, Lagrange usó
los infinitesimales en el cálculo diferencial en el estudio de
fórmulas algebraicas; y en el prólogo a la segunda edición de su obra Mécanique Analytique publicada
en 1811, justifica el empleo de infinitesimales, con estas palabras:
“cuando nosotros hemos cogido el espíritu del método
infinitesimal y lo ha verificado la exactitud de sus resultados por el método
geométrico de primeras y últimas proporciones o por el método analítico de
funciones derivadas, nosotros podemos emplear las cantidades infinitamente
pequeñas como un medio seguro y valiosos de acortar y simplificar nuestras
pruebas”.
Los intereses de Lagrange eran
esencialmente aquellos de un estudiante de matemática pura: buscó y obtuvo
resultados abstractos de largo alcance y estaba satisfecho de dejar las
aplicaciones a otros. De hecho, parte de los descubrimientos de su gran
contemporáneo, Laplace, consiste en la aplicación de las fórmulas de Lagrange a los fenómenos de la naturaleza; por ejemplo, las
conclusiones de Laplace de la velocidad del sonido y de la aceleración secular
de la Luna están ya implícitamente en los resultados de Lagrange.
La única dificultad para entender a Lagrange es el
asunto de interés y la generalidad extrema de sus procesos; pero su análisis es
tan lúcido y luminoso como es simétrico e ingenioso."
Un reciente escritor sobre Lagrange
dice que desempeñó un papel verdaderamente prominente en el avance de casi
todas las ramas de la matemática pura. Como Diofanto y Fermat,
Lagrange poseía un genio especial para la teoría de
números y en este asunto dio soluciones a muchos de los problemas que había
propuesto Fermat y agregó algunos teoremas propios. Creó el cálculo de
variaciones. La teoría de ecuaciones diferenciales está en deuda con él por
convertirla en una ciencia en lugar de una colección de ingeniosos artificios
para la solución de problemas particulares.
Contribuyó al cálculo de diferencias finitas con
la fórmula de interpolación que lleva su nombre. Sus tres trabajos
sobre el método de interpolación de 1783, 1792 y 1793, están actualmente en la
misma fase en que Lagrange los dejó.
PIERRE SIMON LAPLACE
Pierre-Simon
Laplace (1749-1827)
fue un astrónomo, físico y matemático francés que inventó y desarrolló
la transformada de Laplace y la ecuación de Laplace.
Nacido en una familia de granjeros de la
baja Normandía, marchó a estudiar en la Universidad de Caen, donde
fue recomendado a D'Alembert, quien,
impresionado por su habilidad matemática, lo recomendó a su vez para un puesto
de profesor en la Escuela Militar de París en 1767, en la que tuvo entre sus
discípulos a Napoleón Bonaparte. En 1785 es nombrado miembro de la
Academia de Ciencias y en 1795, miembro de la cátedra de matemáticas del Nuevo
Instituto de las Ciencias y las Artes, que presidirá en 1812. En 1788 se casó
con la joven Marie-Charlotte de Courty de Romanges, perteneciente a una familia de Besançon, 20
años más joven que él, y con quien tuvo dos hijos, Sophie-Suzanne
y Charles-Émile. En 1795, Laplace empezó a publicar
el primero de los cinco volúmenes que constituirán su Mecánica celeste y
en 1796 imprime Exposition du système du monde, donde revela su hipótesis
nebular sobre la formación del sistema solar.
En 1799 fue nombrado ministro del Interior
durante el Consulado, aunque no estuvo en el cargo más que seis semanas.
Su antiguo alumno Napoleón Bonaparte le confirió en 1805 la Legión de honor y
en 1806 el título de conde del Imperio. En 1812 publica Teoría
analítica de las probabilidades y en 1814 Ensayo filosófico
sobre la probabilidad. En 1816 fue elegido miembro de la Academia Francesa.
A pesar de su pasado bonapartista, tras la restauración de los Borbones fue
lo bastante hábil como para conseguir ser nombrado marqués en 1817.
En la Exposition
du système du monde (Exposición del
sistema del mundo, 1796) describió una teoría sobre la formación del Sol y
del sistema solar a partir de una nebulosa o remolino de
polvo y gas. Esta hipótesis nebular (la cual ya había sido perfilada
anteriormente por Inmanuel Kant), le da mucho
mayor detalle y múltiples refinamientos, permanece en nuestros días como el
fundamento básico de toda la teoría de la formación estelar. Por otra parte,
demostró también la estabilidad del sistema solar, sentó las bases científicas
de la teoría matemática de probabilidades (en su obra Théorie analytique des probabilités, donde, entre otros logros, formuló el
método de los mínimos cuadrados, que es fundamental para la teoría de errores)
y formuló de manera muy firme e influyente la imagen de un mundo completamente
determinista.
Atento a los descubrimientos de nebulosas realizados
por William Herschel en Inglaterra, Laplace pensó que el colapso
gravitatorio de una nebulosa podría haber dado origen a la formación del Sol y
que el material orbitando en torno al Sol podría condensarse para formar una
familia de planetas. Esta teoría explicaba de manera natural que todos los
planetas orbiten en torno al Sol en el mismo sentido (de oeste a este) y que
sus órbitas estén en un mismo plano. Herschel concordó con esta idea y la
generalizó para explicar la formación y evolución de todas las estrellas y
sistemas estelares.
Es recordado como uno de los máximos científicos de todos
los tiempos, a veces referido como el Newton de Francia, con
unas fenomenales facultades matemáticas no poseídas por ninguno de sus
contemporáneos.
Su obra más importante, Traité
de mécanique céleste (Tratado
de mecánica celeste, 1799-1825, 5 vols.), es un compendio de toda la
astronomía de su época, enfocada de modo totalmente analítico y donde
perfeccionaba el modelo de Newton, que tenía algunos fenómenos pendientes de
explicar, en particular algunos movimientos anómalos que seguían sin
solución: Júpiter estaba sometido a una aceleración aparente,
mientras que Saturno parecía frenarse poco a poco y la Luna también
mostraba un movimiento acelerado. Si estos movimientos continuaban
indefinidamente, Saturno caería sobre el Sol, Júpiter se escaparía del sistema
solar y la Luna caería sobre la Tierra. Con tan sólo 23 años de edad, Laplace
demostró que la aceleración de Júpiter y el frenado de Saturno eran movimientos
periódicos. Los larguísimos períodos (en torno a mil años) habían hecho creer
hasta entonces que estas variaciones eran continuas e indefinidas
('seculares'); en 1785 demostró que tales anomalías se debían a la posición
relativa de Júpiter y Saturno respecto del Sol. Todo ello necesitó una cantidad
enorme de cálculos muy detallados. En 1787 Laplace demostró que el movimiento
anómalo de la Luna también era oscilatorio y que estaba ocasionado por pequeños
efectos (de 'segundo orden') en el sistema triple Sol-Tierra-Luna. Las
variaciones eran periódicas y, por tanto, el sistema solar debía ser estable y
autorregulado. Todas estas ideas se recogieron en su obra Exposition du système
du monde publicada en 1796.
Laplace creó una curiosa fórmula para expresar la probabilidad de
que el Sol saliera por el horizonte. Decía que la probabilidad era de ![]() , donde d es el número de días
que el sol ha salido en el pasado. Laplace afirmaba que esta fórmula, conocida
como la regla de sucesión, podía aplicarse en todos los casos donde no
sabemos algo, o donde lo que conocíamos fue cambiado por lo que no. Aún se usa
como un estimador de la probabilidad de un evento, si sabemos el lugar del
evento, pero sólo tenemos muy pocas muestras de él.
, donde d es el número de días
que el sol ha salido en el pasado. Laplace afirmaba que esta fórmula, conocida
como la regla de sucesión, podía aplicarse en todos los casos donde no
sabemos algo, o donde lo que conocíamos fue cambiado por lo que no. Aún se usa
como un estimador de la probabilidad de un evento, si sabemos el lugar del
evento, pero sólo tenemos muy pocas muestras de él.
Laplace creía fuertemente en el determinismo causal,
tal como puede apreciarse en la siguiente cita:
Podemos mirar el estado presente del universo como el
efecto del pasado y la causa de su futuro. Se podría concebir un intelecto que
en cualquier momento dado conociera todas las fuerzas que animan la naturaleza y
las posiciones de los seres que la componen; si este intelecto fuera lo
suficientemente vasto como para someter los datos a análisis, podría condensar
en una simple fórmula el movimiento de los grandes cuerpos del universo y del
átomo más ligero; para tal intelecto nada podría ser incierto y el futuro, así
como el pasado, estarían frente sus ojos.
Este intelecto se refiere al demonio de Laplace (cf. demonio
de Maxwell). Los descubrimientos de la física moderna, especialmente
la mecánica cuántica y el principio de incertidumbre, prueban que la
existencia de tal intelecto es imposible al menos en principio.
CARL FRIEDRICH
GAUSS

Johann Carl Friedrich Gauss (1777-1855), fue un matemático,
astrónomo y físico alemán que contribuyó significativamente en muchos campos,
incluida la teoría de números, el análisis matemático, la geometría diferencial,
la geodesia, el magnetismo y la óptica. Considerado "el príncipe de las
matemáticas" y "el matemático más grande desde la antigüedad",
Gauss ha tenido una influencia notable en muchos campos de la matemática y de
la ciencia, y es considerado uno de los matemáticos que más influencia ha
tenido en la historia. Fue de los primeros en extender el concepto de
divisibilidad a otros conjuntos.
Johann Carl Friedrich Gauss nació en la ciudad de
Brunswick, Alemania, el 30 de abril de 1777, en una familia muy pobre, su
abuelo era un humilde jardinero de Brunswick. Nunca pudo superar la espantosa
miseria que siempre cargó. De pequeño Gauss fue respetuoso y obediente, y en su
edad adulta nunca criticó a su padre por haber sido tan violento y rudo. Poco
después de que Gauss cumpliera 30 años su padre murió.
Desde muy pequeño Gauss mostró su talento para los números
y para el lenguaje. Aprendió a leer solo, y sin que nadie lo ayudara aprendió
muy rápido la aritmética desde muy pequeño. En 1784 a los siete años de edad
ingresó en la escuela primaria de Brunswick donde daba clases un profesor
llamado Büttner. Se cuenta la anécdota de que a los
dos años de estar en la escuela durante la clase de Aritmética el profesor
propuso el problema de sumar los números de una progresión aritmética. Gauss
halló la respuesta correcta casi inmediatamente diciendo «Ligget
se'» (ya está). Al acabar la hora se comprobaron las soluciones y se vio que la
solución de Gauss era correcta mientras muchas de las de sus compañeros no.
Desde que Gauss conoció a Bartels
sus progresos en Matemáticas se aceleraron. Ambos estudiaban juntos, se apoyaban
y se ayudaban para descifrar y entender los manuales de álgebra y de análisis
elemental que tenían. En estos años se empezaron a gestar algunas de las ideas
y formas de ver las matemáticas que caracterizaron posteriormente a Gauss. Se
dio cuenta, por ejemplo, del poco rigor en muchas demostraciones de los grandes
matemáticos que le procedieron, como Newton, Euler, Lagrange
y otros más. A los 12 años ya miraba con cierto recelo los fundamentos de la
geometría, y a los 16 tuvo sus primeras ideas intuitivas sobre la posibilidad
de otro tipo de geometría. A los 17 años Gauss se dio a la tarea de completar
lo que a su juicio habían dejado a medias sus
predecesores en materia de teoría de números. Así descubrió su pasión por la
aritmética, área en la que poco después tuvo sus primeros triunfos. Su gusto
por la aritmética prevaleció por toda su vida ya que para él “La matemática es
la reina de las ciencias y la aritmética es la reina de las matemáticas”. Gauss
tenía 14 años cuando conoció al duque Ferdinand; éste quedo fascinado por lo
que había oído del muchacho y por su modestia y timidez. Decidió solventar
todos los gastos de Gauss para asegurar que su educación llegara a un buen fin.
Al año siguiente de conocer al duque, Gauss ingresó al Colegio Carolino para
continuar sus estudios, y lo que sorprendió a todos fue su facilidad para las
lenguas. Aprendió y dominó el griego y el latín en muy poco tiempo. Estuvo tres
años en el Colegio Carolino, y al salir no tenía claro si quería dedicarse a
las matemáticas o a la filología. En esta época ya había descubierto su ley de
los mínimos cuadrados, este trabajo marca el interés de Gauss por la teoría de
errores de observación y su distribución.
En 1796 demostró que se puede dibujar un polígono regular
de 17 lados con regla y compás.
Fue el primero en probar rigurosamente el teorema
fundamental del álgebra (disertación para su tesis doctoral en 1799), aunque
una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente.
En 1801 publicó el libro Disquisitiones
Arithmeticae, con seis secciones dedicadas a la Teoría
de números, dándole a esta rama de las matemáticas una estructura
sistematizada. En la última sección del libro expone su tesis doctoral. Ese
mismo año predijo la órbita de Ceres aproximando parámetros por mínimos
cuadrados.
En 1809 fue nombrado director del Observatorio de Göttingen. En este mismo año publicó Theoria
motus corporum coelestium in sectionibus conicis Solem ambientium
describiendo cómo calcular la órbita de un planeta y cómo refinarla
posteriormente. Profundizó sobre ecuaciones diferenciales y secciones cónicas.
Gauss murió en Göttingen el 23
de febrero de 1855.
Obra Maestra
Cubierta de la edición original de Disquisitiones
arithmeticae de Carl Friedrich Gauss, libro
fundamental de la teoría de números.
La primera estancia de Gauss en Gotinga duró tres años,
que fueron de los más productivos de su vida. Regresó a su natal Brunswick a
finales de 1798 sin haber recibido ningún título en la universidad, pero su
primera obra maestra estaba casi lista. La obra estuvo lista a finales del año
1798, pero fue hasta 1801. Gauss la escribió en latín y la tituló Disquisitiones arithmeticae. Por
supuesto, este libro está dedicado a su mecenas, el duque Ferdinand, por quien
Gauss sentía mucho respeto y agradecimiento. Es un tratado de la teoría de
números en el que se sintetiza y perfecciona todo el trabajo previo en esta
área. La obra consta de 8 capítulos pero el octavo no se pudo imprimir por
cuestiones financieras. El teorema fundamental del álgebra establece que un
polinomio en una variable, no constante y a coeficientes complejos, tiene
tantas raíces como su grado.
Carl Wilhelm Ferdinand, duque de Brunswick, a quien Gauss
vivió eternamente agradecido por su invaluable e incondicional apoyo, no solo
fue un protector inteligente de los jóvenes con talento y un cordial
gobernante, sino también un buen soldado. Federico el Grande admiró y estimó
mucho su bravura y el genio militar que demostró durante la guerra de los 7
años que ocurrió entre 1756 y 1763.

Agustín Louis Cauchy
(1789-1857) matemático francés. Cauchy fue pionero en
el análisis matemático y la teoría de grupos de permutaciones, contribuyendo de
manera medular a su desarrollo. También investigó la convergencia y la
divergencia de las series infinitas, ecuaciones diferenciales, determinantes,
probabilidad y física matemática.
Cauchy empezó a educarse tempranamente con su
padre Louis François Cauchy (1760-1848) quien ocupó
varios puestos públicos menores y era amigo de Joseph-Louis de Lagrange y Pierre Simon Laplace.
Estudió en École Polytechnique de París, obteniendo su título en ingeniería.
Por su rendimiento académico brillante, fue contratado como ingeniero militar
en 1812 para contribuir al gran plan de Napoleón para transformar el puerto de Cherbourg en el más importante de Francia e Inglaterra. Sin
embargo, su mala salud le obligó a abandonar este proyecto. Comenzó a dedicarse
a la investigación científica intensiva, y a la publicación de varias obras
importantes en rápida sucesión. La principal conclusión de este período fue la
demostración del teorema del número poligonal de Fermat, al que se habían
dedicado sin éxito ilustres matemáticos contemporáneos como Gauss. Fue nombrado
profesor de la mecánica en la École Polytechnique en 1816. Fue promovido a miembro de la
Academia Francesa de las Ciencias, en lugar de Gaspard
Monge, quien fue expulsado por razones políticas.
En 1830, se vio en la necesidad de seguir siendo fiel al
juramento ante el rey Carlos X por lo que tuvo que abandonar todos sus cargos
académicos y marchar al exilio. Desde París se trasladó a Turín, donde dio
clases en la universidad, y luego se trasladó a Praga, a petición de Carlos X,
como tutor del Conde de Chambord. Regresó a París en
1838, pero no pudo encontrar un lugar en la Sorbona, hasta 1848, cuando fue
nombrado profesor de Astronomía.
En 1814 publicó la memoria de la integral definida que
llegó a ser la base de la teoría de las funciones complejas. Gracias a Cauchy, el análisis infinitesimal adquiere bases sólidas.
Cauchy precisa los conceptos de función, de
límite y de continuidad en la forma actual o casi actual, tomando el concepto
de límite como punto de partida del análisis y eliminando de la idea de función
toda referencia a una expresión formal, algebraica o no, para fundarla sobre la
noción de correspondencia. Los conceptos aritméticos otorgan ahora rigor a los
fundamentos del análisis, hasta entonces apoyados en una intuición geométrica
que quedará eliminada, en especial cuando más tarde sufre un rudo golpe al
demostrarse que hay funciones continuas sin derivadas, es decir: curvas sin
tangente. Cauchy consideraba que las funciones en 3
dimensiones que eran derivables eran continuas sin embargo se descubrió que era
necesaria una condición de diferenciabilidad para
asegurar la continuidad. Pesa sobre el hecho de que estando en la Universidad
se adjudicaba teoremas que pertenecían a los alumnos, denominando los teoremas
en conjunto con los alumnos que irremediablemente debían de presentar sus
trabajos ante Cauchy.
En 1832 fue nombrado miembro de la Royal Society y en 1845 de la Royal Society
of Edinburgh.
Existe un cráter lunar con su nombre (Cauchy).
BERNARD BOLZANO
Bernard Placidus
Johann Gonzal Nepomuk
Bolzano (1781-1848), conocido
como Bernard Bolzano fue
un matemático, lógico, filósofo y teólogo bohemio,
nacido en Praga, en el reino de Bohemia, actualmente República Checa, que
escribió en alemán y que realizó importantes contribuciones a las
matemáticas y a la Teoría del conocimiento.
En matemáticas, se le conoce por el teorema de
Bolzano, así como por el teorema de Bolzano-Weierstrass,
que esbozó como lema de otro trabajo en 1817 y décadas después habría de
desarrollar Karl Weierstrass.
En su filosofía, Bolzano criticó el idealismo de Hegel y Kant afirmando
que los números, las ideas y las verdades existen de modo
independiente a las personas que los piensen.
En 1796 Bolzano se inscribió en la Facultad de
Filosofía de la Universidad de Praga. Durante sus estudios escribió:
"Mi especial predilección por las Matemáticas se basa de modo
particular en sus aspectos especulativos, en otras palabras, aprecio mucho la
parte de las Matemáticas que es al mismo tiempo Filosofia."
En otoño de 1800 empezó a estudiar Teología. Se dedicó a ello los
siguientes tres años, durante los que también preparó su tesis doctoral en
Geometría. Consiguió el doctorado en 1804, tras haber redactado una tesis
en la que expresaba su opinión sobre las Matemáticas y sobre las
características de una correcta demostración matemática. En el prólogo
escribió: "No podría sentirme satisfecho por una demostración
estrictamente rigurosa, si ésta no derivase de los conceptos contenidos en la
tesis que debe demostrarse."
Dos años después de ser nombrado doctor, Bolzano se ordenó
como sacerdote católico romano. Sin embargo, su auténtica vocación era la
docencia y en 1804 obtuvo la cátedra de Filosofía y Religión en la
Universidad de Praga. En relación con esta cátedra hay que señalar que en
aquella época, por la expansión del entusiasmo suscitado por la Revolución
francesa, se habían desarrollado los primeros movimientos políticos que
reivindicaban la libertad de pensamiento y la independencia de las comunidades
nacionales. Estas reivindicaciones preocupaban mucho a los estados autoritarios
y en especial al Imperio austríaco, en cuyos límites se integraban
numerosos grupos étnicos muy distintos, entre los que iban naciendo movimientos
nacionalistas. Para contrarrestar estos movimientos, el Imperio austríaco, de
acuerdo con la Iglesia católica, que estaba claramente alineada en
posiciones conservadoras frente a las procedentes de la revolución francesa,
llevaba a cabo una serie de iniciativas. Entre estas, estaba la de instituir
una cátedra de Filosofía de la Religión en cada Universidad, que se erigiera
como baluarte contra la libertad de pensamiento y contra las posiciones
nacionalistas.
Sin embargo, la designación de Bolzano para ocupar dicha
cátedra en la Universidad de Praga no tuvo el éxito que las autoridades
esperaban. Sus enseñanzas estaban impregnadas por fuertes ideales pacifistas y
por una viva exigencia de justicia política. Además, Bolzano gozaba, debido a
sus cualidades intelectuales, de un enorme prestigio entre sus colegas
profesores y entre los estudiantes. Tras algunas presiones del gobierno
austríaco, en 1819 Bolzano fue destituido de su cátedra. Debido a su
personalidad, no aceptó este cese sin manifestar su desacuerdo, con lo que se
le suspendió, bajo una acusación de herejía, puesto bajo arresto
domiciliario y se le prohibió publicar. A pesar de la censura del gobierno, sus
libros se publicaron fuera del Imperio austríaco y Bolzano siguió escribiendo y
ocupando un importante papel dentro de la vida intelectual de su país.
Bolzano escribió en 1810 Beiträge
zu einer begründeteren Darstellung der Mathematik. Erste Lieferung, la primera de una serie programada de
escritos sobre fundamentos de las matemáticas. En la segunda parte,
encontramos Der binomische Lehrsatzl... de 1816 y Rein analytischer Beweis... (Pura demostración matemática) de 1817,
que contienen un intento de impostación del cálculo infinitesimal que no
recurre al concepto de infinitesimal. En el prólogo del primero de ambos
declara que su trabajo es un ejemplo del nuevo modo de desarrollar el análisis.
A pesar de que Bolzano consiguió demostrar exactamente todo lo que declaraba,
sus teorías sólo se entendieron después de su muerte. En el trabajo de 1817
Bolzano entendía que liberaba los conceptos de límite, convergencia y derivada
de nociones geométricas, sustituyéndolas por conceptos puramente aritméticos y
numéricos. Bolzano era consciente de la existencia de un problema más profundo:
era necesario refinar y enriquecer el propio concepto de número. En este
trabajo hay que situar la demostración del teorema del valor intermedio con
la nueva aproximación de Bolzano y la que también fue llamada serie de Cauchy. Este concepto es tratado en un trabajo de Cauchy, publicado cuatro años después, aunque resulta poco
probable que el matemático francés conociera los trabajos de Bolzano.
Después de 1817, Bolzano estuvo muchos años sin publicar
nada relacionado con las matemáticas. Sin embargo, en 1837, publicó Wissenschaftslehre, un intento de elaborar una
teoría del conocimiento y de la ciencia completa. Bolzano intentó proporcionar
fundamentos lógicos a todas las ciencias, construidas partiendo de
abstracciones, de objetos abstractos, de atributos, de construcciones de
demostraciones, vínculos... La mayor parte de esos intentos retoman esos
trabajos anteriores que afectan a la relación objetiva entre las consecuencias
lógicas (las cosas tal como se producen) y nuestra percepción puramente
subjetiva de dichas consecuencias (nuestro modo de abordar los hechos). Aquí se
acerca a la filosofía de las matemáticas. Para Bolzano, no tenemos ninguna
certeza en cuanto a las verdades o a las supuestas como tales, de la naturaleza
o de las matemáticas y precisamente el papel de las ciencias, tanto puras como
aplicadas, es hallar una justificación de las verdades (o de las leyes)
fundamentales, que con frecuencia contradicen nuestras intuiciones. Muchos
estudiosos, entre los que se encuentra Edmund Husserl, consideran este texto,
como la primera obra importante sobre lógica y problemas de conocimiento tras
la de Leibnitz.
Entre 1830 y 1840, Bolzano trabajó en una
obra mayor, Grössenlehre en la que
tratará de reinterpretar toda la matemática bajo bases lógicas. Sólo llegó a
publicar una parte, esperando que sus alumnos prosiguieran su obra y publicaran
una versión completa. En 1854, tres años después de su muerte, un alumno
suyo publicó la obra de Bolzano Paradoxien
des Unendlichen, un estudio sobre las paradojas
del infinito. Aparece por primera vez el término "conjunto", en la
forma alemana Menge. En este trabajo Bolzano
aporta ejemplos de correspondencia biunívoca entre los elementos de un conjunto
infinito e incluso de un subconjunto.
La mayor parte de los trabajos de Bolzano permaneció en
forma de manuscrito, por lo que tuvo una circulación muy reducida y una escasa
influencia en el desarrollo de la materia. Muchas de sus obras no se publicaron
hasta 1862 e incluso después. Las teorías de Bolzano sobre el infinito matemático
anticiparon a las de Georg Cantor sobre conjuntos infinitos.

Carl Gustav Jacob Jacobi (1804-1851)
fue un matemático alemán, autor muy prolífico, contribuyó en varios
campos de la matemática, principalmente en el área de las funciones
elípticas, el álgebra, la teoría de números y
las ecuaciones diferenciales. También destacó en su labor pedagógica, por
la que se le ha considerado el profesor más estimulante de su tiempo.
Jacobi estableció con Niels Henrik Abel la Teoría de las funciones Elípticas.
Demostró la solución de integrales elípticas mediante la aplicación de las
funciones y las series exponenciales introducidas por él mismo.
Desarrolló los determinantes funcionales, llamados después
jacobianos y las ecuaciones diferenciales.
El padre de Jacobi era banquero
y su familia era muy próspera, fue así como él recibió una buena educación en
la Universidad de Berlín. Obtuvo su Doctorado en 1825 y enseñaba matemáticas en
Koningsberg desde 1826 hasta su muerte, fue
denominado para una cátedra en 1832.
En 1834 probó que si una función univaluada
de una variable es doblemente periódica, entonces la razón de los periodos es
imaginaria. Este resultado impulsó enormemente el trabajo en esta área, en
particular por Liouville y Cauchy.
Jacobi tenía la reputación de ser un
excelente maestro, atraía a muchos estudiantes. Introdujo un método de
seminario para enseñar a los estudiantes los últimos avances matemáticos.
Jacobi nació en Potsdam en 1804 en el seno de
una familia judía en Alemania. Su padre era un próspero banquero y su
hermano mayor, Moritz Jacobi,
llegaría a ser un físico eminente. Un tío materno se encargó de su educación
con éxito, pues en 1817, en cuanto entró en el Gymnasium
a la edad de 11 años, le situaron en el último curso. Sin embargo, en la Universidad
de Berlín la edad mínima de acceso era de 16 años, por lo que su ingreso
tuvo que esperar hasta 1821. Durante los años en los que permaneció en el Gymnasium destacó también en griego, latín e historia.
Para cuando finalmente empezó sus estudios universitarios,
ya había leído y asimilado los trabajos de eminentes matemáticos como Euler y Lagrange e incluso había empezado a investigar una forma de
resolver ecuaciones de quinto grado, por lo que el nivel de las clases le
pareció bajo y siguió estudiando por su cuenta fuera de las aulas. En 1824, a
pesar de ser judío, se le ofreció una plaza como profesor en una prestigiosa
escuela de enseñanza secundaria de Berlín.
En 1825 presentó su tesis doctoral, una discusión
analítica de la teoría de fracciones. Como la enseñanza universitaria
estaba vetada a los judíos, decidió convertirse al cristianismo, tras lo
que obtuvo una plaza como Privatdozent. Para entonces
contaba con 20 años. Tras un año en la Universidad de Berlín y ante la carencia
de posibilidades de promoción decidió, aconsejado por sus colegas, trasladarse
a Königsberg (actual Kaliningrado, Rusia)
en 1826, donde se encontraría con Franz Neumann y Friedrich Bessel, que por aquel tiempo tenía un gran prestigio en
matemáticas y astronomía.
Una vez en Königsberg se puso en
contacto con Gauss para informarle de su trabajo sobre los residuos
cúbicos y escribió a Legendre acerca
de sus resultados en el área de las funciones elípticas. Ambos quedaron
impresionados por el talento del joven Jacobi. En
1829 publicó Fundamenta nova theoria functionum ellipticarum trabajo
en el que asentó nuevas bases para el análisis de funciones elípticas,
fundamentado en el uso de la función theta de Jacobi,
que había desarrollado recientemente y que fue nombrada en su honor. Sus
trabajos en este campo gozaron del apoyo de Legendre,
el mayor experto de la época en funciones elípticas, lo que le facilitó optar por
la plaza de profesor asociado. Los principios que había establecido habían sido
desarrollados de forma independiente por el matemático noruego Niels Henrik Abel, con el que entablaría una cierta competición
que resultó ser muy beneficiosa para las matemáticas y que se interrumpiría
debido al temprano fallecimiento de Abel en 1829, a la edad de 27 años. Durante
el verano de ese año, Jacobi realizaría un viaje a
París durante el cual se reuniría con algunos de los más eminentes matemáticos
de su tiempo: Fourier, Poisson y Gauss.
En 1831 contrajo matrimonio con Marie Schwinck.
Dos años más tarde, su hermano Moritz se fue a vivir
también a Königsberg. La influencia de su hermano
mayor le causó un gran interés por la física. Durante esta época trabajó
principalmente en ecuaciones diferenciales y determinantes,
estudiando, entre otros asuntos, el concepto que hoy en día se conoce
como jacobiano. Publicó el fruto de estos años
en su obra: Sobre la formación y propiedades de los determinantes.
En 1842 visitó Cambridge y Mánchester junto
con Bessel, en representación de Prusia,
invitado por la Asociación Británica para el Avance de la Ciencia. A su vuelta
dio una conferencia en la Academia de Ciencias Francesa. Se hizo célebre
su respuesta a la pregunta de, quién, a su juicio, era el matemático vivo más
grande de Inglaterra, que le formularon a su regreso: «No hay ninguno».
Al preguntarle sobre su extraordinaria dedicación a su trabajo contestó «Ciertamente,
algunas veces he puesto en peligro mi salud a causa del exceso de trabajo pero
¿y qué? Solamente los vegetales carecen de nervios y preocupaciones. ¿Y qué
obtienen de su perfecto bienestar?». Al año siguiente, probablemente a
causa del exceso de trabajo, su salud empeoró y se le diagnosticó diabetes.
El medicó le aconsejó mudarse a Italia, donde el clima era más benigno.
Por aquel tiempo Prusia estaba sumida en una grave crisis
económica y, pese a que Jacobi había nacido en una
familia rica, otro matemático, Dirichlet tuvo
que interceder, ayudado por Alexander von Humboldt, ante Federico
Guillermo IV de Prusia para que éste ayudara económicamente a Jacobi. En Italia recobró la salud y se dedicó al estudio
de la Arithmetica de Diofante. En 1844 volvió a Berlín, donde el clima no era
tan extremo como en Königsberg. En los años venideros
se apreciaría un cambio en el punto de vista de Jacobi,
que pasaría a interesarse más por los aspectos físicos de la mecánica,
abandonando la interpretación puramente axiomática que había desarrollado Lagrange.
En 1848, a consecuencia del derrocamiento de Luis
Felipe I de Francia en París, se desencadenó una serie de movimientos
revolucionarios que sacudieron Europa, conocidos como las revoluciones de
1848. Jacobi dio en Berlín un discurso político que
disgustó tanto a republicanos como a monárquicos, lo que trajo
como resultado que le vetaran para la enseñanza en Berlín y más tarde le
retiraran la ayuda económica que le permitía permanecer allí, por lo que Jacobi decidió mudarse a Gotha.
Más tarde se le restablecería parte de la asignación económica, que le
permitiría volver a dar clases en Berlín, aunque su familia permanecería en Gotha. En 1851 contrajo una gripe que le debilitó
gravemente. Poco tiempo más tarde contraería viruela, enfermedad que le llevaría
a la muerte pocos días después.

George Green (1793-1841) fue
un matemático inglés cuyo trabajo influenció notablemente el
desarrollo de importantes conceptos en física. Entre sus obras más famosas
se cita: "Un análisis de las aplicaciones del análisis matemático a las
teorías de la electricidad y el magnetismo" publicado en 1828. En
este ensayo se introdujeron los conceptos de funciones de potencial utilizados
comúnmente en la formulación matemática de la física. También aparecieron en
este ensayo las funciones de Green y aplicaciones importantes del teorema
de Green.
Green fue un científico autodidacta. Vivió la mayor parte
de su vida en Sneinton, Nottinghamshire,
actualmente parte de la ciudad de Nottingham. Su
padre, también llamado George, era un panadero que poseía un molino de viento
para preparar la harina. El joven George Green solo asistió de forma regular a
la escuela durante un año entre los 8 y 9 años de edad, ayudando a su padre
posteriormente.
En algún momento comenzó sus estudios de matemáticas. Al ser
Nottingham un pueblo pobre en recursos intelectuales,
no se ha podido dilucidar por parte de los historiadores de dónde obtenía Green
la información necesaria para su desarrollo en matemáticas. Solo se conoce una
persona que haya vivido en Nottingham durante esa
época, con los suficientes conocimientos matemáticos: John Toplis. Cuando Green publicó su ensayo en 1828, fue vendido
como una suscripción a 51 personas, la mayoría de las cuales eran probablemente
amigos y sin ninguna idea de sobre matemáticas.
El acaudalado terrateniente y matemático Edward Bromhead compró una copia y animó a Green a ir más
lejos en su trabajo matemático. Sin embargo, Green no confió en su mentor y no
volvió a contactar con él durante dos años.
Luego de esos dos años, Bromhead
realizó las gestiones para que Green ingresara a la Universidad de
Cambridge. Green ingresó como estudiante a la edad de 40 años. Su carrera
académica fue excelente y tras de su graduación en 1837 permaneció en la
facultad, en la Escuela Gonville y Caius. Escribió sobre óptica, acústica e hidrodinámica
y a pesar que sus escritos posteriores no tuvieron la relevancia de su Ensayo
de 1828, de igual manera fueron muy reputados. Los trabajos de Green sobre
el movimiento de las olas en un canal, anticipa la aproximación WKB de
la mecánica cuántica, mientras que su investigación sobre ondas lumínicas y de
las propiedades del Éter producían lo que hoy es conocido como
las Medidas de deformación de rotación independiente. En 1839 fue
electo miembro de la junta directiva de la escuela; que disfrutaría los
privilegios del cargo por un corto tiempo, pues en 1840 cae enfermo y regresa a
Nottingham, donde muere un año después.
El trabajo de Green fue poco conocido en la comunidad
matemática durante su vida. En 1846, su trabajo fue redescubierto por un
joven William Thomson, quien lo hizo popular entre los futuros matemáticos
de la época.
En la actualidad, la Biblioteca George Green de la Universidad de Nottingham alberga gran parte de su obra en la
colección de ciencias e ingeniería de la universidad. En 1986, el molino de los
Green fue restaurado, ahora funciona como museo y centro científico.
En una visita a Nottingham en
1930, Albert Einstein comentó que Green estuvo 20 años adelantado a
su época. El físico teórico Julian Schwinger, quién usó parte de la obra de Green en su
trabajo sobre investigación de avanzada, publicó un tributo titulado "The Greening of Quantum
Field Theory: George and I".

George Gabriel Stokes (1819-1903) fue un matemático y
físico irlandés que realizó contribuciones importantes a la dinámica de fluidos
(incluyendo las ecuaciones de Navier-Stokes), la
óptica y la física matemática (incluyendo el teorema de Stokes). Fue secretario
y luego presidente de la Royal Society de Inglaterra.
George Stokes fue el hijo menor del Reverendo Gabriel
Stokes, rector de Skreen, en el condado de Sligo.
Allí nació y creció George, en el seno de una familia protestante evangélica.
Después de haber estudiado en Skreen, Dublín y
Bristol, George se matriculó en 1837 en Pembroke College, en la Universidad de Cambridge, donde cuatro años
más tarde, tras graduarse con los más altos honores, fue elegido para ocupar
una plaza de profesor. George Stokes ocupa esta plaza hasta 1857, cuando se ve
obligado a renunciar a ella por haber contraído matrimonio (ambas cosas eran
incompatibles según los estatutos de su facultad universitaria). Sin embargo,
doce años más tarde, tras haber sido modificados los estatutos, es reelegido.
Ocuparía dicha plaza hasta 1902, año en el que fue promocionado a la mastership de su facultad. No obstante, no podría gozar
demasiado de esta posición, pues moriría en Cambridge el 1 de febrero del año
siguiente.
En 1849 le fue concedida la Cátedra Lucasiana
de matemáticas de la Universidad de Cambridge. George Stokes, que fue nombrado
baronet en 1889, también sirvió a su universidad representándola en el
parlamento desde 1887 hasta 1892, como uno de los dos miembros de la Cambridge University Constituency. Durante
parte de este periodo (1885-1890) fue presidente de la Royal Society, de la que había sido secretario desde 1854, y de
esta manera, siendo a la vez Profesor Lucasiano, unió
en sí mismo tres cargos que sólo en una ocasión habían estado en manos de un
solo individuo, Isaac Newton, quien, no obstante, no ocupó las tres
simultáneamente.
Stokes fue el mayor del trío de filósofos naturales, los
otros dos fueron James Clerk Maxwell y Lord Kelvin, que contribuyeron
especialmente a la fama de la escuela de Cambridge de física matemática a
mediados del siglo XIX. El trabajo original de Stokes empezó en 1840, y desde
ese año en adelante la gran cantidad de trabajo que produjo fue solamente
superada por la brillantez y enorme calidad del mismo. El catálogo de artículos
científicos de la Royal Society muestra los títulos
de más de cien contribuciones hechas por él hasta 1883. Algunas de éstas son
sólo notas breves, pero la mayoría son tratados largos y elaborados.
El trabajo de Stokes se distingue por su precisión y su
sentido de la finalidad. Incluso en problemas que en su tiempo no se
consideraban susceptibles de análisis matemático, Stokes fue capaz en muchos
casos de aportar soluciones que dejaron sentadas las bases para el progreso
posterior. Este hecho se explica por su extraordinaria combinación de capacidad
matemática y habilidad experimental. Desde el momento en que, sobre 1840, puso
a punto sus primeros aparatos físicos simples en Pembroke
College, matemáticas y experimento siempre fueron de
la mano, ayudándose y controlándose mutuamente. Su trabajo abarcó un amplio
abanico de cuestiones físicas, pero, como Marie Alfred Cornu
remarcó en su conferencia [Rede]] de 1899, la mayor parte del mismo versó sobre
ondas y las transformaciones sufridas por éstas al pasar a través de varios
medios.
Sus primeros artículos publicados, que aparecieron en 1842
y 1843, trataban del movimiento uniforme de fluidos incompresibles y algunos
casos de movimiento fluido. A éstos les siguió uno en 1845 sobre la fricción de
fluidos en movimiento y el equilibrio y movimiento de sólidos elásticos y en
1850 otro sobre los efectos de la fricción interna de los fluidos sobre el
movimiento de los péndulos. También realizó varias contribuciones a la teoría
del sonido, incluyendo una discusión del efecto del viento sobre la intensidad
del sonido y una explicación de cómo la intensidad es influenciada por la
naturaleza del gas en cuyo seno se produce el sonido. Estas investigaciones
sentaron las bases de la ciencia de la hidrodinámica y proporcionaron claves no
sólo para la explicación de muchos fenómenos naturales, tales como la
suspensión de las nubes en el aire o el hundimiento de las olas en el agua,
sino también para la solución de problemas prácticos, como el flujo de agua en
ríos y canales o la resistencia al movimiento de los barcos.
Su labor en relación al movimiento de los fluidos y la
viscosidad le llevó a calcular la velocidad terminal de una esfera que cae en
un medio viscoso, lo cual pasó a conocerse como la ley de Stokes. Más adelante
la unidad CGS de viscosidad pasaría a llamarse el Stokes, en honor a su
trabajo.
Quizá sus investigaciones mejor conocidas son las
referentes a la teoría ondulatoria de la luz. Sus trabajos sobre óptica
empezaron pronto en su carrera científica. Los primeros artículos sobre
aberración de la luz aparecieron en 1845 y 1846 fueron continuados en 1848 por
uno sobre la teoría de ciertas bandas del espectro electromagnético. En 1849
publicó un largo trabajo sobre la teoría dinámica de la difracción, en el cual
mostraba que el plano de polarización debe ser perpendicular a la dirección de
propagación. Dos años después trató de los colores de placas gruesas.
En 1852, en su famoso trabajo sobre el cambio en la
longitud de onda de la luz, describió el fenómeno de la fluorescencia, tal y
como la mostraban la fluorita y el cristal de uranio, materiales que él vio
como capaces de convertir la invisible radiación ultravioleta en radiaciones de
mayor longitud de onda, visibles. El desplazamiento de Stokes, que describe
dicha conversión, es llamado en su honor. A continuación, un modelo mecánico
que ilustraba el principio dinámico de la explicación de Stokes fue propuesto y
de éste surgió el concepto de línea de Stokes, que a su vez es la base de la
dispersión Raman. En 1883, durante una conferencia en
la Royal Institution, Lord Kelvin dijo que Stokes le
había contado este fenómeno muchos años atrás y que él le había insistido, en
vano, para que lo publicara.
Ese mismo año, 1852, apareció el artículo sobre la
composición y resolución de corrientes de luz polarizada de distintas fuentes y
en 1853 una investigación de la reflexión metálica exhibida por ciertas
sustancias no-metálicas. Hacia 1860 se metió en un estudio sobre la intensidad
de la luz reflejada o transmitida a través de una pila de placas y en 1862
preparó un valioso informe para la Asociación Británica para el Avance de la
Ciencia (BAAS) sobre la doble refracción. De la misma fecha es un artículo
sobre el largo espectro de la luz eléctrica, que a su vez fue seguido por un
análisis del espectro de absorción de la sangre.
La identificación de compuestos orgánicos mediante sus
propiedades ópticas fue tratada en 1864 y, más tarde, junto con el Reverendo
William Vernon Harcourt, investigó la relación entre
la composición química y las propiedades ópticas de varios cristales, con
referencia a las condiciones de transparencia y la mejora de los telescopios
acromáticos. Otro trabajo posterior también conectado con la construcción de
instrumentos ópticos discutía los límites teóricos de la apertura de los
objetivos de los microscopios.
En otros campos de la física cabe mencionar sus trabajos
sobre la conductividad térmica en cristales (1851) y sobre el radiómetro de Crookes; su explicación del borde claro a menudo observado
en las fotografías justo por fuera del perfil de un cuerpo oscuro visto con el
cielo de fondo (1883); y, más tarde aún, su teoría de los rayos X, de los que
sugirió que podían ser ondas transversales viajando como incontables ondas solitarias,
en lugar de como trenes de ondas regulares. Dos largos artículos publicados en
1840, uno sobre atracciones y el teorema de Clairaut,
y el otro sobre variaciones en la gravedad de la superficie terrestre, también
merecen ser mencionados, así como sus trabajos matemáticos sobre valores
críticos de sumas de series periódicas (1847), cálculos numéricos de una clase
de integrales definidas y series infinitas (1850) y su discusión de una
ecuación diferencial relativa a la ruptura de puentes de ferrocarril (1849).
Además de sus abundantes trabajos publicados, Stokes
realizó múltiples descubrimientos que jamás llegaron a publicarse, o como mucho
fueron comentados brevemente en alguna de sus conferencias orales. Un ejemplo
excelente lo constituye su trabajo sobre la teoría de la espectroscopia. En su
conferencia presidencial a la BAAS en 1871, Lord Kelvin afirmó su creencia de
que la aplicación del análisis prismático de la luz a la química solar y
estelar no había sido planteada directa o indirectamente por nadie cuando
Stokes se la enseñó a él en Cambridge antes del verano de 1852. Estas
afirmaciones hacen suponer que Stokes se anticipó a Gustav Robert Kirchhoff
como mínimo siete años en la enunciación de las bases físicas sobre las que
descansa la espectroscopia y la identificación de sustancias en el sol y las
estrellas. Stokes, sin embargo, en una carta publicada unos años después de la
conferencia de Lord Kelvin, dijo que él no había sido capaz de efectuar un paso
esencial en su razonamiento (no se había percatado de que la emisión de luz de
longitud de onda definida no sólo permitía, sino que requería, absorción de luz
de la misma longitud de onda). Modestamente, Stokes negó haber tomado
"parte alguna en el admirable descubrimiento de Kirchhoff", añadiendo
que algunos de sus amigos lo habían defendido excesivamente. No obstante, debe
decirse que los científicos británicos no están del todo convencidos de esta
negación y todavía atribuyen a Stokes el mérito de haber sido el primero en
formular los dos principios fundamentales de la espectroscopia.
Todavía en otro sentido Stokes contribuyó grandemente al
progreso de la física matemática. Poco después de ser elegido para la cátedra Lucasiana anunció que consideraba su deber profesional
ayudar a cualquier miembro de la universidad en problemas matemáticos con que
se pudiesen encontrar. La ayuda prestada fue tan real que los alumnos, incluso
después de haberse convertido en sus colegas, no tenían ningún inconveniente en
consultarle sobre los problemas matemáticos y físicos que les causaban
dificultades. Más adelante, durante los treinta años en los que actuó como
secretario de la Royal Society también ejerció una
enorme, aunque no reconocida, influencia sobre el avance de las ciencias
matemáticas y físicas, no sólo directamente por sus propias investigaciones,
sino también indirectamente sugiriendo problemas para investigar y animando a
gente para enfrentarse a ellos.
![]()
Karl Theodor Wilhelm Weierstrass
(1815-1897) fue un matemático alemán que se suele citar como el padre del
análisis moderno.
Hijo de un oficial a las órdenes de Napoleón, Karl era el
mayor de cuatro hermanos. Más tarde, su padre ingresó en el servicio de
recaudación de impuestos en Prusia, lo que obligó a la familia a trasladarse
constantemente.
Con catorce años, Karl fue aceptado en la escuela católica
de enseñanza secundaria de Paderborn. Ganó algunos
premios antes de graduarse y en 1834, siguiendo los deseos de su padre, ingresó
en la Universidad de Bonn para estudiar comercio y finanzas; sin embargo, estas
materias no le interesaban y pasó la mayor parte del tiempo bebiendo,
practicando esgrima y leyendo libros de matemáticas.
En 1839 fue aceptado en la Academia de Teología y
Filosofía de Münster, donde encontró la inspiración
matemática de manos de Christof Guderman.
Éste le introdujo en la teoría de las series de potencias, que más tarde serían
la base de todo su trabajo. Su primer escrito importante, publicado en 1841,
fue un ensayo sobre funciones elípticas.
Durante los quince años siguientes se dedicó a dar clase
en una escuela de enseñanza secundaria. En 1854 envió un trabajo sobre
funciones abelianas a una publicación matemática de
prestigio y sorprendió a la comunidad matemática con su genio. Por este trabajo
recibió el doctorado honorífico de la Universidad de Königsberg
y en 1856 fue aceptado como profesor asociado en la Universidad de Berlín.
Abrumado por las enormes responsabilidades de su nuevo
cargo, sufrió una crisis nerviosa en 1861, que le apartó de las aulas dos años.
A pesar de ello, en 1864 fue ascendido a profesor, cargo que ostentó el resto
de su vida. Desafortunadamente, tras los ataques públicos de Kronecker por su apoyo a las ideas de Cantor y la muerte de
su amiga Sonja Kovalevsky,
se hundió mentalmente y pasó el resto de su vida en una silla de ruedas hasta
que murió víctima de una neumonía.
Además de sus prolíficas investigaciones cabe señalar que
fue profesor de cátedra en la Universidad de Berlín en la cual tuvo entre sus
discípulos a Georg Cantor, Ferdinand Georg Frobenius,
Wilhelm Killing, Leo Königsberger,
Carl Runge, Sofia Kovalévskaya y Edmund Husserl.
Weierstrass dio las definiciones de continuidad,
límite y derivada de una función, que se siguen usando hoy en día. Esto le
permitió demostrar un conjunto de teoremas que estaban entonces sin demostrar
como el teorema del valor medio, el teorema de Bolzano-Weierstrass
y el teorema de Heine-Borel. También realizó aportes
en convergencia de series, en teoría de funciones periódicas, funciones
elípticas, convergencia de productos infinitos, cálculo de variaciones,
análisis complejo, etc.

Jean Frédéric Frenet (1816-1900) fue un famoso matemático francés que
introdujo la Teoría de Curvas junto a Joseph Serret.
En reconocimiento a su trabajo, se denomina a la base espacial definida por los
vectores tangente, normal y binormal, triedro de Frenet-Serret.
Nació en Périgueux, Francia en
1816 y en el año 1840 ingresó en L’École Normale Superieure, más tarde
continuó sus estudios en Toulouse, ciudad en la que redactó su tesis doctoral
durante 1847. Un fragmento de la mencionada tesis alberga la teoría de curvas
en el espacio, incluyendo las fórmulas que actualmente son conocidas como
‘fórmulas de Frenet – Serret’.
Frenet aportó seis de dichas fórmulas, mientras que Serret proporcionó las nueve restantes. Cabe señalar que Frenet publicó este apartado de su tesis en el ‘Journal de mathématique pures et appliques’, en el año
1852.
Frenet llegó a ser profesor en Toulouse y en
1848 ocupó un puesto de docente de matemáticas en Lyon. Además, también fue
director del observatorio astronómico, donde dirigió las observaciones
meteorológicas.
El libro de ejercicios sobre cálculo de Frenet, cuya primera edición fue publicada en 1856, ha
tenido siete ediciones, la última de ellas divulgada en 1917.
JOSEPH ALFRED SERRET

Joseph Alfred Serret (1819-1885),
más conocido como Joseph Serret, fue un matemático francés
famoso por desarrollar junto a Jean Frenet la teoría
de curvas.
Graduado por la École polytechnique en 1840 y miembro de sus tribunales de
admisión desde 1848; en 1861 fue nombrado profesor de Mecánica celeste en el Collège de France y diez años después obtuvo la cátedra de
Cálculo Diferencial e integral en la Sorbonne. Joseph
formó parte también del Bureau des Longitudes desde 1873.
La principal aportación de Serret
en el ámbito de las matemáticas se produjo dentro de la geometría diferencial.
Junto a Charles Bonnet y Bertrand Russell realizó importantes avances en esa
cuestión, elaborando las fórmulas Frenet-Serret,
fundamentales en la teoría de las curvas espaciales.
También trabajó algunos aspectos de la teoría de números,
el cálculo y la mecánica. Editó los trabajos de Lagrange
—publicados en catorce volúmenes entre 1867 y 1892— y realizó la quinta edición
de Monge en 1850. Una de sus principales obras fue el manual Cours d'Algèbre supérieure, editado en dos tomos.
En 1860 ocupó el lugar de Poinsot
en la Académie des Sciences
de Francia. En 1871, ante el progresivo deterioro de su salud, se retiró a Versailles hasta su fallecimiento en 1885.

Georg Friedrich Bernhard Riemann
(1826-1866) fue un matemático alemán que realizó contribuciones muy importantes
al análisis y la geometría diferencial, algunas de las cuales allanaron el
camino para el desarrollo más avanzado de la relatividad general. Su nombre
está conectado con la función zeta, la hipótesis de Riemann, la integral de
Riemann, el lema de Riemann, las variedades de Riemann, las superficies de
Riemann y la geometría de Riemann.
Nació en una aldea cercana a Dannenberg,
en el Reino de Hanóver, actualmente parte de Alemania.
Su padre Friedrich Bernhard Riemann era pastor
luterano en Breselenz y había luchado en las guerras
napoleónicas. Bernhard era el segundo de seis hermanos,
su frágil salud y la temprana muerte de casi todos sus hermanos fueron debidas
a la subalimentación en su juventud. Su madre también murió antes de que sus
hijos crecieran.
En 1840 Bernhard fue a Hanóver a vivir con su abuela y a visitar el Lyceum. Después de la muerte de su abuela en 1842 entró al Johanneum Lüneburg. Desde pequeño
demostró una fabulosa capacidad para el cálculo unido a una timidez casi
enfermiza. Durante sus estudios de secundaria aprendía tan rápido que enseguida
adelantaba a todos sus profesores.
En 1846, a la edad de 19, comenzó a estudiar filología y
teología en la Universidad de Göttingen, su idea era
complacer a su padre y poder ayudar a su familia haciéndose pastor. Acudió a
conferencias de Gauss sobre el Método de mínimos cuadrados. En 1847 su padre
reunió el dinero suficiente para que comenzara a estudiar matemáticas.
En 1847 se trasladó a Berlín, donde enseñaban Jacobi, Dirichlet y Steiner. En
1848 estallaron manifestaciones y movimientos obreros por toda Alemania,
Riemann fue reclutado por las milicias de estudiantes, incluso ayudó a proteger
al rey en su palacio de Berlín. Permaneció allí por dos años y volvió a Göttingen en 1849.
En 1859, al doctorarse en matemáticas ante Gauss, formuló
por primera vez la hipótesis de Riemann la cual es uno de los más famosos e
importantes problemas sin resolver de las matemáticas.
Riemann dio sus primeras conferencias en 1854, en las
cuales fundó el campo de la geometría de Riemann. Lo ascendieron a profesor
extraordinario en la universidad de Göttingen en 1857
y se hizo profesor ordinario en 1859. En 1862 se casó con Elise
Koch. Murió de tuberculosis en su tercer viaje a Italia en Selasca.
Dentro de los trabajos más sobresalientes de Riemann se
pueden citar los siguientes:
Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen complexen Grösse (Conceptos
básicos para una teoría general de las funciones de variable compleja, 1851).
Publicado en Werke: Disertación sobre la teoría
general de funciones de variable compleja, basada en las hoy llamadas
ecuaciones de Cauchy-Riemann. En ella, inventó el
instrumento de la superficie de Riemann.
Ueber die Darstellbarkeit
einer Function durch eine trigonometrische
Reihe (Sobre la representación de una función por una
serie trigonométrica, 1854) Publicado en Werke:
Realizado para acceder a su cargo de Profesor auxiliar y en el cual analizó las
condiciones de Dirichlet para el problema de
representación de funciones en serie de Fourier. Con este trabajo, definió el
concepto de integral de Riemann y creó una nueva rama de las matemáticas: La
teoría de funciones de una variable real.
Ueber die Hypothesen,
Welche der Geometrie zu Grunde liegen
(Sobre las hipótesis en que se funda la geometría, 1854) Publicado en Werke: Transcripción de una clase magistral impartida por
Riemann a petición de Gauss la cual versa sobre los fundamentos de la
geometría. Se desarrolla como una generalización de los principios de la
geometría euclidiana y la no euclídea. La unificación
de todas las geometrías se conoce hoy en día como geometría de Riemann y es
básica para la formulación de la Teoría de la Relatividad de Einstein.
Ueber die Anzahl
der Primzahlem unter einer gegebenen Grösse (Sobre el número de primos menores que una cantidad
dada, 1859) Publicado en Werke: El más célebre
trabajo de Riemann. Su único ensayo sobre la teoría de números. La mayor parte
del artículo está dedicado a los números primos. En ella introduce la función
zeta de Riemann.
En nuestro idioma, existe una edición de escritos
matemáticos, físicos y filosóficos de Riemann: Riemanniana
Selecta, editada por J. Ferreirós (Madrid, CSIC,
2000; colección Clásicos del Pensamiento). Se incluyen los tres últimos
trabajos mencionados, además de otros materiales, precedidos por un estudio
introductorio de unas 150 páginas.
ANTOLOGÍA ELABORADA POR:
FRANCISCO
BARRERA GARCÍA
2015
FUENTES BIBLIOGRÁFICAS Y
MESOGRAFÍA
ENCICLOPEDIA
ENCARTA 2009
http://www.portalplanetasedna.com.ar
http://fejer.ucol.mx/ricardo/?p=541
http://www.biografiasyvidas.com/
http://loffit.abc.es/2012/08/18/george-green-las-matematicas-iletradas/69609
Nota: Este trabajo de compilación es con fines académicos y no lucrativos.



